The Secret of the Greek Miracle: An Analysis of the Harmonics in
Archytas' Doubling of the Cube
by Drew Hempel, MA
Wherein I present a hitherto unknown harmonic solution to Archytas
discovery of the continuum, the basis for the Greek Miracle.
Professor K Saito in his essay "Doubling the cube : a new
interpretation of its significance for early Greek geometry", Historia
Math. 22 (2) (1995), 119-137 notes that "Strangely enough, in contrast
to the abundance of solutions for inserting two mean proportionals, we
have little testimony on how Hippocrates' reduction was proved in
antiquity." Saito establishes that the usual proof presented for
doubling the cube ( i.e. WR Knorr) is not accurate since the technique
used was actually a process Saito calls "reduction to linear ratio."
Saito warns against the usual projection of modern mathematics onto
Archytas' proof: "At any rate, one should be wary of invoking the use
of the multiplicate and compound ratios in reconstructing early Greek
geometry, since these methods appeared to have been developed later
and are not directly supported by pre-Euclidean documentary evidence."
The proofs given for doubling the cube have thus far relied on
techniques that leave out the connection between the continued
fraction of Hippocrates and the multiplication of ratios as magnitude,
discovered by Eudoxus and used by Archytas. For example
Professor Barnabas B. Hughes in his essay "Hippocrates and Archytas
Double the Cube," The College Mathematics Journal, 1989:
"Unfortunately, Hippocrates did not say how the two mean proportionals
were to be found." Even Saito, while giving the geometric foundation
for Hippocrates' continued proportion proof, does not elaborate on how
the continued proportion, A:X::X:Y::Y:2A was then used algebraically
for doubling the cube. This later technique of continuum, based on
dynamics, is nothing less than the "Greek Miracle" itself, yet there
remains a vital missing link. As math Professor Luigi Borzacchini notes on the Historia Matematica listserve:
"In other words when music theory paved the road toward the discovery
of incommensurability the idea of geometric magnitude was too clumsy to
develop and even to understand such discovery, and it was exactly the
possibility of the
geometric drawing of a not-existent music interval to foster the
development of the Aristotelean continuity." (that's his unedited
Italian to English comment from "Music and Incommensurability", Luigi
Borzacchini, Wed, 18 Aug 1999).
Professor Borzacchini introduced online his research on music and
incommensurability, what he called the possible "secret of the sect."
There followed a very engaged discussion of this issue, including David
Fowler, author of The Mathematics of Plato's Academy, with one
mathematician, Robert Tragesser, noting that Karl Popper starts a book
by emphasizing the central role of music in the discovery of
incommensurability. To understand the importance of this music
"vanishing mediator" for science we should consider that, in contrast
to the relatively modern dynamic continuum relying on irrational magnitude, the
use of infinitesimals, for calculus, has been traced by Professor
Abraham Seidenberg back to 1800 BC, in Egypt, India, Babylon and China.
(A. Seidenberg, "On the Volume of a Sphere," Archive for History of
Exact Sciences, 1988, published posthumously). Professor Saito, in a
follow-up analysis, goes so far as to debunk the mainstream
interpretation of pre-Eudoxan analysis of proportions in
his "Phantom Theories of pre-Eudoxean Proportion," Science in Context
(2003). In other words Heath and all the other science commentaries
on Euclid are wrong. Saito states: "Heath's...position could be more
consistent if he extended this argument to the whole of Books V and
VI. In fact, these books can be better understood as description and
justification of techniques in geometry concerning proportion, not as
presentation of theorems about ratio and proportion in the abstract."
But it is recognized that the main technique used for the "reduction
to linear ratio" proof was the use of music ratios yet the details has
thus far been ignored, although Professor Luigi Borzacchini raised the
issue and he responded, by mail, to a preliminary music proof I sent
him back around 2001. Professor Michael Allen in his book Nuptial
Arithmetic: Marsilio Ficino's Commentary on the Fatal Number in Book
VIII of Plato's 'Republic' (1994) gives direct evidence for how music
ratios were the central idea in launching modern science. Stuart
Isacoff's book Temperament details how the ratio 5/4, as an extension
of the Pythagorean Tetrad, was the key for the Renaissance, since it
approximates the value cube root of two. This conversion of music
ratios to irrational fraction is further analyzed by music Professor
Emeritus Ernest McClain in his book The Pythagorean Plato as well as
Burkert who emphasizes the "reduction to linear ratio" technique:
"The important thing in Pythagorean musical theory was not the
function of the proportion but the meaningful numbers," Professor
Walter Burkert ( Lore and Science in Ancient Pythagoreanism ,
1972:400).
David Fowler notes in his Mathematics of Plato's Academy: "...the
manipulations of music theory seem to depend fundamentally on the
operation of compounding, an operation which seems to pose some serious
problems for mathematicians. My purely speculative suggestion...is that
music theory might plausibly give some help with this problem." (p.
146). Fowler certainly takes a close look at the connection between
continued ratio and the concept of compounding proportions which later
lead to incommensurability but again no direct music ratios are plugged
into the equation. He states, "In the event, it will turn out that this
contribution from music to mathematics is negligible or non-existent,
but nevertheless the idea is worth trying." (p. 138).
So let's try again.
What we are given for the continued proportion are the phonetic
symbols of the ratios, attributed to the sides of the cubes. So the
online essay "Duplication of the Cube," from McGill University
mathematicians, Francois Rivest and Stephane Zafirov, notes:
Hippocrates showed that the problem could be reduced to that of finding
two mean proportionals: if for a given line segment of length a it is
necessary to find x such that x cubed = 2a cubed, line segments of
lengths x and y respectively may be sought such that a:x = x:y = y:2a;
for then a cubed/x cubed = (a/x) cubed = (a/x)(x/y)(y/2a) = a/2a =
1/2. Pamela Brister in her 1995 online mathforum article on Duplicating
the Cube notes: "Hippocrates of Chino (a Pythagorean mathematician) in
440 BC ... declared that the problem could be solved if 2 successive
mean proportional line
segments were found between a given segment and another twice its
length. He gave the equation a : x = x : y = y : 2*a. Hence if a is
the side of the original cube, then x = cubic root(2*a) is the side of
it's volumetric double. Unfortunately, Hippocrates did not say how the
2 mean proportionals were to be found...." University of St. Andrews
math department gives the same description, again without the actual
numbers plugged into the equation: "(i) To find a cube whose ratio to
a given cube equals the ratio of two given lines. Now Hippocrates
reduced the problem to the following: (ii) Given two lines, find two
mean proportionals between them. i.e. given lines a, b find x, y such
that a : x = x : y = y : b. Now it is easy with our modern
understanding of ratio to see that (i) and (ii) are equivalent. For
a cubed : x cubed = (a:x) cubed = (a : x)(x : y)(y :B)= a : b. Thus
if we are given a cube with side a and want to construct a cube b : a times
the volume, we need to construct the cube of side x." And finally, just
to really clarify this trick business of compounding ratios, here's
how Wilber Richard Knorr's The Ancient Tradition of Geometric
Problems (1986) describes the equation: "Hippocrates' insight is of
course not restricted to lines assumed in a 2:1 ratio. If for any two
given lines, A and B, we can insert the two mean
proportionals, X and Y, then A:X = X:Y=Y:B. Thus, by compounding the
ratios, one has (A:X)cubed = (A:X)(X:Y)(Y:B), that is, A cubed:X cubed
= A:B. Thus, X will be the side of a cube in the given ratio (B:A) to
the given cube (A cubed)."
It's this key value in the continued proportion, A:X::X:Y::Y:2A with X
as the cube root of two that gives the lead for the music ratio
solution. Normally this connection between the harmonic proportions
and the geometric solution is not made but Bruce Director in his
online book Riemann for Anti-Dummies, clarifies the connection: "As
can be seen from the solutions to doubling the cube by Archytas and
Menaechmus, the harmonic relationship among these powers reflects a
characteristic curvature, that, when projected onto straight lines,
produces the relationships the Pythagoreans recognized as the
arithmetic, geometric and sub-contrary, (or harmonic) means. The
arithmetic mean is three numbers related by a common difference: c - a
= b - c, or, c = 1/2 (a+B). Geometrically, it is represented by the
half-way point along a line; musically it corresponds to the interval
of the fifth. The geometric mean is three numbers in constant
proportion: a:b::b:c. Geometrically it is represented by the middle
square between two squares; musically it corresponds to the Lydian
interval. The harmonic mean is the inverse of the arithmetic mean: 1/c
= 1/2(1/a+1/b). It is expressed geometrically in the hyperbola and
musically by the interval of the fourth. These harmonic relationships
are number shadows cast by the curved onto the straight. (See Riemann
for Anti-Dummies 33. EIR website.)
When it's contended that the "Pythagoreans recognized" the harmonic,
geometric and arithmetic means there must be the correction that in
fact these means were the innovation of Archytas to create the Greek
Miracle. Dr. Alan C. Bowen details how Archytas developed these means
from Pythagorean harmonics (from "The Minor Sixth (8:5) in Early Greek
Harmonic Science", by Alan C. Bowen, The American Journal of Philology, 1978:
"Archytas defined the genera of the tetrachord by a procedure
involving the division of the fifth (3:2) into a minor third (6:5) and
a major third (5:4), and of the fourth (4:3) into a septimal third
(7:6) and a major tone (8:7)....The fifth is partitioned according to
an arithmetic mean (3:2=6:5:4) and the fourth, according to a harmonic
mean (4:3=28:24:21).
"In other words, the minor sixth is derivable from the fifth because
it is a major third less than an octave [(2/1)/(5/4) = (8/5)] and a
minor third more than a fourth [(8/5)/(6/5) = (4/3)]."
Archytas could not use 5:8 (the ratio of the minor Sixth as measured
by frequency, not string length) because he had to extend the harmonic
ratios to beyond the octave in order to derive the minor sixth and
perfect 4th. As Bowen states, "For it was during this time that scales
of a double octave magnitude, i.e. the Greater Perfect System, were
constructed to facilitate the analysis of melody." The Greater Perfect
System, using two octaves, was the extension of the ratios by Archytas
as a transition to magnitude since now the middle of the octave,
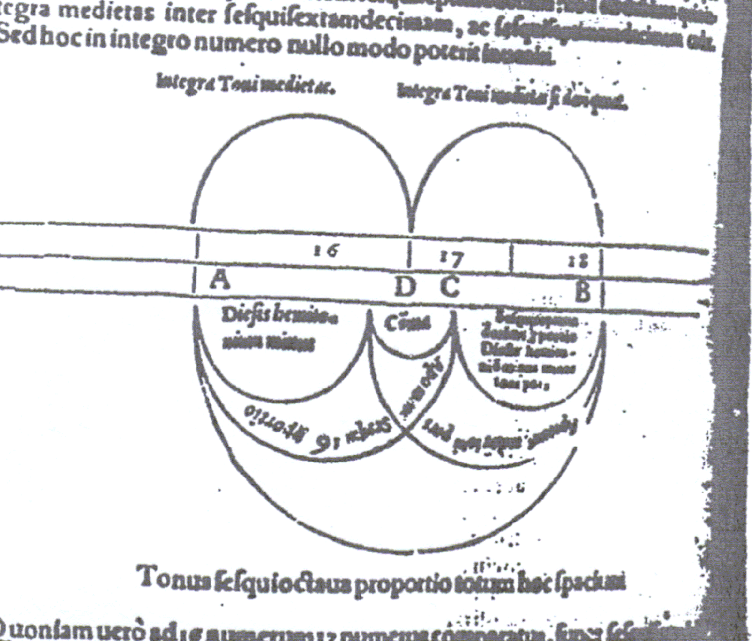
normally the irrational square root of two as 9/8 cubed, could be turned into just 2:1.
Dr. Bowen clarifies:
"Any who doubt that the musical ratios are all of greater inequality,
i.e., that the antecedent or first term in each is greater than the
consequent or second term, should consult Archytas DK 47 B 2. This
Fragment requires that the ratios be of this form if the assertions
about the three means [arithmetic, harmonic and geometric] are to be
true. Accordingly, the ratios assigned to the octave, fifth, fourth
and minor sixth, must be 2:1, 3:2, 4:3 and 8:5, and not 1:2, 2:3, 3:4
and 5:8, respectively, as Mosshammer and others would have
them. Indeed, there is early proof deriving from the Pythagorean
school that intervals, such as the fifths, which are represented by
superparticular ratios cannot be partitioned into any number of equal
subintervals because the terms of these ratios admit no number of
geometric means. Consider now the question of the status of the ratio
(8:5) in the Pythagorean harmonic science that dates from the late
fifth century B.C. to the time of Apollodorus. One should not expect
that this ratio was recognized as melodic by every school of
Pythagorean musical theory. For example those who sought to derive
all the musical ratios from the Tetrad of the decad by compounding and
dividing the ratios of the primary and most familiar intervals, the
concords of the octave, fifth and fourth, would find the minor sixth
unascertainable.There is reason to believe that these were supplied
by Archytas in the early fourth century B.C."
At this juncture it should be pointed out that the interval of the fifth
as the arithmetic mean, while representing geometrically the midpoint
of a line ( 1.5), in fact is the value 2/3 -- not 1/2. Conversely while
the geometric mean is represented as "the middle square between two
squares," musically it is the midpoint of a line or string (what should
be the arithmetic mean) -- the tritone interval between the fifth and
the fourth. I clarify this incongruity because it appears that the
Greek Miracle depends on a conversion, an actual changing of the number
order from 5:8 to 8:5 so that symmetric phonetic symbols have
commutative correspondance with number, at the expense of the actual
geometric value of the asymmetric harmonics found in the Law of
Pythagoras. Only when the interval of the fifth, as the arithmetic mean,
is extended to the octave plus the fifth, is the harmonic, as the
interval twelve, a symmetrical reduction of the line or string into
thirds.
Here's how H. Steinhaus describes the difference in his Mathematical
Snapshots: "Between F and G lies F-sharp (the black key in the very
center of the octave): the ratio between C and F-sharp is the same as
between F-sharp and high C, amounting to an augmented fourth. If we
call x the ratio F-sharp:C, we get x squared = 2, hence x = square root
of two, which is an irrational number." (p. 44).
To give further background for the derivation of the asymmetric Law of
Pythagoras, the natural overtones, here's how Professor Michael Hudson
describes the difference of arithmetic and geometric progression in music:
"Archytas emphasized that there were different kinds of proportion.
Simple arithmetic proportion is characterized by the progressions 1, 2,
3, 4, or 2, 4, 6, 8. Each number in the series stands an equal distance
from the next. On a graph this progression appears as a straight
line.... But this is not how musical scales
work. Whatever the key or clef, the relative proportions among the
intervals and string lengths remain constant as they are transposed
higher or lower. Each octave is double the frequency (or half the
string length) of the tonic ( i.e., from C to C' or from G to G'),
while the interval of the fifth (C to G, or C' to G') sounds always in
the ratio of 3:2. Musical intervals rise by a process of
multiplication (and descend by division). Thus, the proportions
between the intervals remain constant, being doubled or otherwise
multiplied in the ratio 2, 4, 8, 16 and so forth. This is known as
geometric proportion. On a chart, this exponential series looks like
an ascending wave."
Professor Michael Hudson continues: "An octave can be doubled by
multiplying by twos, but this will only generate the same note on
every higher frequencies. To generate the entire scale by means of the
Circle of Fifths (3/2), the number three is needed. The musician
proceeds from C to G, and then to D, by multiplying 3/2 by 3/2 = 9/4.
The octave of "4" is 8; hence, 9/4 (D'/C) = 9/8 (D'/C'). The entire
circle of fifths may be generated by keeping even powers of 2 (i.e.,
2n) in the denominator, while the numerator is expanded by 3p."
"Music as an Analogy for Economic Order in Classical Antiquity" by Dr.
Michael Hudson, in Jürgen Backhaus (ed.), Karl Bücher. Theory,
History, Anthropology, Non-Market Economies (Marburg:Metropolis Verlag
2000): pp. 113-35
So we can see that the ratio 9/8 was created only after the octave was
doubled for the purpose of geometric mean. Although the later
Pythagoreans used the ratio 9/8 for tuning it must be emphasized that
the early Pythagoreans did not use the D' above the octave. Why?
Because the ratio 9/4,
reduced to 9/8, is not of the Tetrad. As Professor Andre Barbera
notes: "Orthodox Pythagorean theory recognizes five consonances:
fourth, fifth, octave, twelfth, and double octave; and these are
represented by the
multiple and superparticular ratios from the tetrad. The number 8
obviously does not belong to the tetrad." from "The Consonant Eleventh and
the Expansion of the Musical Tetractys: A Study of Ancient
Pythagoreanism," by André Barbera, Journal of Music Theory, 1984.
Barbera does note that Archytas used the Babylonian tetrachord, an
extension of the tetrad, 6:8::9:12 whereby 8 is the geometric mean and
9 is the arithmetic mean between 6 and 12. We see further
confirmation that this use of 9:8 is an innovation of Archytas and Eudoxus in
"Pythagorean Mathematics and Music," by Richard L. Crocker, The
Journal of Aesthetics and Art Criticism, 1963. Crocker notes that
R. P. Winnington-Ingram's, "Aristoxenos and the Intervals of
Greek Music," (1932) as an article "admits that the pre-Platonic theorists
used the tone 8:9 to construct a scale, but for some reason is reluctant to
attribute this construction to the pythagoreans."
We can see a close analogy between the Hippocratic continued
proportion used for doubling the cube, A:X::X:Y::Y:2A and the tetrachord
from Babylonian math, 6:8::9:12. It is in this analogy that the
original symmetry between phonetic letters and number arose because in
"orthodox" Pythagoreanism C to G is 2:3 while G to C is 3:4, in
violation of the commutative prinicple. And indeed Archytas applied his
equation whereby the Arthmetic Mean times the Harmonic Mean equals the
Geometric Mean squared in order to double the cube. Plugging in the
values 1 and 2 for A and B the GM is the square root of two,
approximated as 9/8 cubed, giving a music interval proof for
incommensurability.
For further clarification let's quote a Truman State University review
on Scriba, Christoph J. "Mathematics and music." (Danish) Normat 38
(1990), no. 1, 3--17, 52:
"The author discusses the relationship between mathematics and music
from Pythagorean through modern times. His story begins in in
Pythagorean times, and as he explains, the notes of the musical scale
were then determined by the ratio of a perfect fifth, i.e. 3:2. Twelve
intervals of a fifth are roughly equal to seven octaves, but are in
reality slightly more than seven octaves, the discrepancy being the
"Pythagorean comma" of 312:219, or roughly 74:73. Whole steps in the
scale were in the ratio 9:8, and half steps were in the ratio 256:243.
Thus two half steps were slightly less than one whole step. In fact,
Philolaus noted that one whole note is equal to two half notes plus a
Pythagorean comma. Archytas showed that intervals like the octave 2:1,
fifth 3:2, fourth 4:3, and whole tone 9:8, or any other interval in
the ratio (n+1):n cannot in fact be divided with rational numbers into
two equal intervals. However, he noted that the product of the
arithmetic mean and the harmonic mean is equal to the square of the
geometric mean, so this gave a way of dividing the fifth of 3:2 into
the product of 5:4 and 6:5. 5:4 can be thought of as a major third,
and 6:5 can be though of as a minor third. So the ratio 3:2 is divided
as 6:5:4. Similarly, the fourth of 4:3 can be divided into the product
of 7:6 and 8:7, so the ratio 4:3 is divided as 8:7:6. The interval 7:6
can be though of as a shrunken minor third and 8:7 can be though of as
an enlarged whole tone. Scriba suggests that the germs of the idea of
making this division lie with the Babylonians."
Now finally we can proceed to the actual continued proportion proof
using music harmonics. If the cube root of two is the value for X and
if the cube root of two was approximated as the music ratio 5/4 then
A:X::X:Y::Y:2A with A as 1 and 2A as 2 and X as the cube root of two
gives the following result. By doubling the octave to 4, so that
Archytas could apply his geometric mean, the continued proportion of
Hippocrates can also be cubed so that A is 1 and 2A is 8 and the
proportion is 1:2::2:4::4:8. Since the cube root of this equation
means that X equals 5/4 then the cube root of four, as Y, gives the
harmonic ratio of 8:5, the complimentary opposite of 5/4 (the
major Third, 5/4, is inverted as the minor Sixth, 8:5).
1:5/4::5/4:8/5::8/5:2.
That's the secret of the Greek Miracle -- converting Pythagorean
harmonics into the continuum.
It should be noted that the Golden Ratio A:B::B:A + B must
have the order reversed to A - B for a quadratic solution using zero.
The Harmonic Mean also does not work if zero is used. For the 8:5
Pentgram as the original origin for the discovery of incommensurability,
via "mutual subtraction" of side lengths using the 60-based number
system (and not the continued proportion Pythagorean Theorem proof in
Euclid) see, "The Discovery of Incommensurability by Hippasus of
Metapontum," by Kurt Von Fritz, The Annals of Mathematics, 1945. The
Fibonacci Number series, 1,1,2,3,5,8 must have its order reversed to 8:5
(see H.E. Huntley's Divine
Proportion) to achieve the quadratic-based irrational Golden Ratio --
for the same reason that enabled Archytas to approximate the square
root of two as 9/8 cubed, and to double the cube, using 5/4. Robert
Lawlor's book Sacred Geometry gives further connections between music,
Archytas, and the Golden Ratio.
The Golden Ratio, which "governs black holes" (Dr. Mario Livio), and is
found in special relativity, can now be seen to arise from the inversion
of the minor Sixth music interval, from 5:8 to 8:5. This simple
harmonics analysis of the doubling of the cube reveals a paradox in
symmetry that appears to be on the order of Heisenberg's discovery of
uncertainty. As Guy Murchie describes in his book Music of the Spheres,
Heisenberg considered extremely long radio waves but they would be
blind to the position of the electron since energy is proportional to
frequency. From uncertainty came Max Born's discovery of the violation
of the commutative principle, just as in the Pythagorean Tetrad whereby C
to G is 2/3 and G to C is 3/4. More recent applications of nonlinear
resonance enables the creation of acoustoelectric energy from the
pressure of bones. Maybe the orthodox Pythagorean shamans were correct
after all.
Kepler's use of 3/5 (Major Sixth), from the Golden Ratio pentagram, and
5/4, based on sacred geometry applied to music, was then considered to
the basis for his "major and minor modes" of the Solar System. The
extension of his sacred circle-equilateral tetrad symbol to 5/4 creates
an ellipse -- due to the inherent complimentary opposite principles that
Kepler found in the Golden Ratio method of exhaustion proof. (for
futher discussion see, "Kepler's Celestial Music," by D. P. Walker,
Journal of the Warburg and Courtauld Institutes, 1967).
Bruce J. Brackenridge sums up the mystery of asymmetry in his article,
stating: "Thus the pentagon is the archetypal figure of generation
itself." ("Kepler, elliptical orbits, and celestial circularity: A
study in the persistence of metaphysical commitment," Annals of Science,
Volume 39, Number 2, March 1982 , pp. 117-143).
Although I couldn't find which of Sir Karl Popper's 50 books kicks off
with an ode to Pythagorean music as the key to incommensurability I did
discover a kicker from one of his final speeches: "Of all Schrodinger's
precursors, Kepler is the only one who foresaw that harmony - resonance
- holds the world together." (from All Life is Problem Solving by Karl
Popper, Routledge, 1999, p. 75).