Acoustic Alchemy: You said that the Daoists only utilised 4/3 (yin) and 3/2 (yang) because together they both add together to create the octave, but did they not make use of other ratios too?

The heart is called Yi [unified power] becuz when intent moves, spirit is agitated; qi is dispersed. Qi is the Mother of spirit; Spirit is the child of qi. The Mother as qi is the horse that guides/conducts the river chariot (yin spirit) in the water (yin jing). Once your mind is away from the lower Elixir Field, your Qi will be led away from it and be consumed. By gathering the Shen into the lower tan tien then the Qi follows it there. Light of eyes descend as Yang fire inner yin qi line

Sunday, April 29, 2018

You said that the Daoists only utilised 4/3 (yin) and 3/2 (yang) because together they both add together to create the octave, but did they not make use of other ratios too?

Quote

By contrast, Schellenberg & Trehub (1994a,b, 1996a,b) attempted to explore the possibility that the special perceptual status of intervals with simple frequency ratios derives from a natural or inherent biological basis. This was achieved by evaluating infants' ability to detect subtle changes to patterns of simultaneous and sequential pure tones. Their results confirmed that simple, as opposed to complex, frequency ratios are more readily identified by listeners and consequently are more likely to result in a stable perceptual representation. As this was true even for infants, the perceptual status of these special intervals is unlikely to be due to education or exposure to Western musical practices.

So the key point here about the Daoists and Early Pythagoreans and the three gunas of India - is that it is noncommutative phase - meaning 2:3 is C to G as overtone (3/2 frequency) and 2/3 is C to F undertone - BOTH as Perfect Fifth but the octave as the root tonic changes when you double the C to F undertone as 2/3 into 4/3 so that now the "3" is the root tonic instead of the "1" and since 3 does not go into 1 as the same pitch (unlike 2) then you have the empirical truth of infinite yin-yang without any materialistic root tonic as the 1. And so the first harmonic of F is C - so that the "yin" as 4/3 is actually from the yang as 2/3 subharmonic C to F - since the overtone F reaffirms the root tonic of C as it is the first tonic of F. This is not true for the G. This is the secret female formless awareness of Mystery of the Valley - Qi is the Mother of spirit. The 1 is the spirit that is not a number since light is invariant to time and space but the 2/3 is superluminal to light as a spacetime blue-shift of light.

Quote

However, as the frequency ratio P : Q becomes more ‘complicated’, the two tones share fewer common harmonics, while there is an increase of harmonic pairs slightly mismatched in frequency. According to Helmholtz's (1877) linear theory, these latter nearby harmonics interact and lead to an unpleasant beating sensation that results in dissonance.

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2607353/

So Western music theorists will try to argue that the infinite spiral of fifths is no different than say an infinite spiral of thirds - but that is because standard western math assumes a symmetric logarithm and ignores the noncommutative phase truth.

So now it's been shown that neuron synchronization is strongest from the octave/perfect fifth/perfect fourth:

Quote

the ordering of the stability index of the mode-locked states and reveals a correspondence with the theoretical ordering of musical intervals according to their consonance evaluation. The ordering corresponds to ratio simplicity discussed in Schellenberg & Trehub (1994b), where the simplest ratios (e.g. 1 : 1, 1 : 2, 2 : 3) are the most consonant.

Maybe I already posted that image?

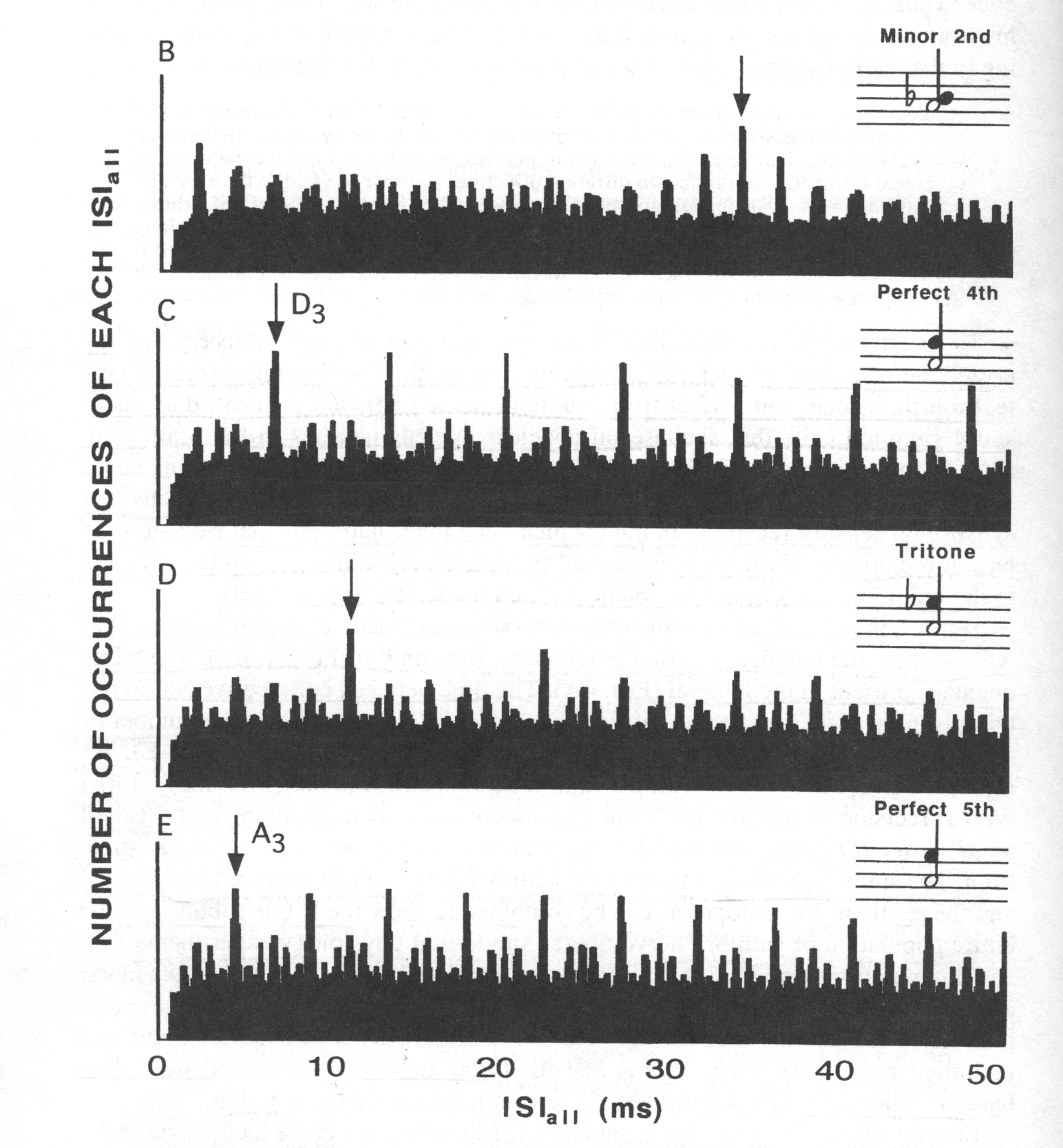
O.K. so those studies are limited to the neurons whereas the quantum biology model goes down to the microtubules that make up the neurons - and then you get into superluminal time as quantum spin or reverse time phase from the magnetic moment of the electron and proton.

So Dr. Andrija Puharich first discovered that model in quantum biology and it's now being corroborated. And Dr. Stuart Hameroff and his collaborator in Japan - I have corresponded with both of them - they emphasize that in fact these quantum vibrations are "anharmonic" meaning NOT Western logarithmic music tuning, but in fact the tuning of Indian raga music or the three gunas as the natural resonance of the Octave/Perfect Fifth/Perfect Fourth. haha. So that is a slam dunk for the Daoist harmonics as well - and of course all human cultures back to the original San Bushmen (it's not the Western symmetric logarithmic math from the wrong music tuning that is predicated on a "deep preestablished disharmony" as math professor Luigi Borzacchini calls it).

No comments:

Relativistic Quantum physicist protege of Olivier Costa de Beauregard:

"Then comes the question: What would the de jure allowed, but de facto repressed, direct information-to-negentropy transition look like, and consist of? Well, such a phenomenon is nothing less than the one termed either 'precognition' or 'psychokinesis' in parapsychology....Why, then, if such phenomenon do exist, are they so alien to our Western culture, while, as it seems, they are alien neither to the more 'primitive' cultures nor to the elaborate cultures of the 'Far East'?..." Olivier Costa de Beauregard, protege of Nobel Physicist Louis de Broglie. "Do you know what the really brilliant piece of work here is? It's de Broglie! It's tremendous imagination. To find there are TWO oscillations where are EVERYWHERE AND IN ALL TIME IN PHASE AND YET IN DIFFERENT FREQUENCIES: THEY MOVE THROUGH ONE EACH other seemlessly - it's magnificient!" Martin van der Mark on the Law of Phase Harmony and why all matter is made of light due to 1/2 spin as Law of Phase Harmony: "the mean internal frequency of the photon will increase; simultaneously the orbital frequency of the photon will decrease due to the relativistic law of the slowing down of clocks." (see below for more details)

Orthodox Pythagorean philosophy=Daoist Neigong (noncommutative Eddie Oshins)

"However, even in this case there is a highly non-commutative world of higher order collectivity algebras B(n). This can be used to capture the geometry of rotations, like those appearing in the classical Pythagorean octave versus perfect fifth considerations." Music of Quantum Circles October 2017 DOI:10.1007/978-3-319-47337-6_11 In book: The Musical-Mathematical Mind (pp.99-110) Professor Micho Đurđevich https://www.matem.unam.mx/~micho/inde... Institute of Mathematics, UNAM, Mexico citing Alain Connes: "a non-commutative algebra naturally engenders a one-parameter group of automorphisms that makes it evolve, that makes it rotate in such a way that the passage from xy to yx corresponds to what evolution yields for the purely imaginary value t = sqrt(-1) of the parameter t of the evolution group. We must ... introduce evolution only after choosing a state in the algebra, but the evolution obtained is modified only by inner automorphisms and these are in a certain sense invisible. Here, I believe, is the key link that Hamilton sought between time and algebra. ..." In the book "Triangle of Thoughts" (American Mathematical Society, 2001) Alain Connes, Andre Lichnerowicz, and Marcel Paul Schutzenberger discuss the interrelationships among Mathematics, Physics, and Philosophy.

each zero point of geometry already has yin/yang as future (yang movement)/past (yin stillness)

As for O it is the "two emblems." O is the movement of yang. O is the stillness of yin.

The "O" will not be translated as Li included the symbol to refer to a reality at once underlying the three teachings and yet standing outside the categories of each teaching's doctrinal discourse.

p. 29

https://open.library.ubc.ca/media/download/pdf/831/1.0092419/1

PDF link on Ph.D. thesis on
Li Dao-Chun (李道純) was a 13th century Daoist Master in the line of the famous 4th generation Master of the southern Nei Dan lineage, Bai Yuchan. Li is author of the Zhōng Hé Jí (中和集) translated as Anthology on the Center and Harmony.

Resonance of Reality: Natural harmonics as natural numbers proven as Inverse Doppler Effect

Ancient Acoustic Alchemy of Pan instruments: flute, pipe, clarinet, recorder: "A fossil of flute discovered in Germany dated back to 25,000 years ago26. In contrast, it wasn’t until 1842 when the Doppler effect was first introduced to public, while the property of inverse Doppler effect may have been utilized for thousands of years. The bandwidth of conventional negative refraction metamaterials is inherently limited by the local resonance. However, the pipe instruments exhibit different negative refractive indices over a wide range of frequencies. It therefore can be used as a basic unit for designing various novel smart broadband acoustic metamaterials...This type of metamaterial is composed of Helmholtz resonators of which the group and phase velocities are opposite in direction near the resonant frequency."

Ancient Noncommutative Phase Natural Resonance proven as left-handed meta-material music

Transverse or Inverse Doppler Effect from Ancient Acoustic Alchemy music: " the theory of effective medium is only related to the size in the Y-Z plane and has no connection with the size along the X-axis. Along the Y-axis, the lattice constant (2.7 cm) of the sample is determined by the tube (0.7 cm in diameter) and the sponge substrate (2.0 cm in thickness). Along the Z-axis, there is a one-to-one correspondence between the meta-molecules with different lengths and sound waves with different wavelengths. For instance, the meta-molecule with a length of 9.8 cm corresponds to the sound wave with a wavelength of approximately 20 cm; the meta-molecule with a length of 2.9 cm corresponds to the sound wave with a wavelength of approximately 6 cm."

Tang Dynasty alchemy meditation

高上玉皇胎息經/Gaoshang Yuhuang Taixi Jing -The Most High Jade Emperor's Embryonic Breathing Classic

玉皇天尊曰:
Jade Emperor Tianzun said:

胎從伏氣中結, 氣從有胎中息。
The embryo comes from the Qi hidden away while breathing, Qi comes from having the embryo while breathing.

氣入身來謂之生, 神去離形謂之死。
Qi entering the body & arriving is called birth, Shen going & leaving the body is called death.

知神氣, 可以長生。
Knowing Shen & Qi, long life is possible.

故守虛無, 以養神氣。
Therefore, guard nothingness in order to cultivate Shen & Qi.

神行即氣行, 神住即氣住。
When the Shen moves then the Qi circulates, where the Shen stops then the Qi dwells.

若欲長生, 神氣相注。
If you desire a long life, mutually focus the Shen & Qi.

心不動念, 無來無去, 不出不入, 自然常在。
When the Xin isn't moved by thoughts, lacking coming & lacking going, without exiting & without entering, it will, naturally, always stay.

勤而行之, 是真道路。

Constantly practicing it is the true path of the Dao.

"When high energy substances of the subconscious mind emerges, they should be one's guiding force."

qigong master Yan Xin

Qigong Master Chunyi Lin on antigravity qigong levitation secret: "The essence [jing] of the metal is the sound and the essence [yuan jing] of the earth. That is from the universe [yuan qi] as the gravity when you breathe in the energy from this five elements perspective you breathe in that vibration from gravity, you feel that energy filling you up." http://springforestqigong.com

The MetaMaterial Universe - google book preview link on image

Noncommutative Phase MetaMaterial as de Broglie Law of Phase Harmony..." materials with negative refractions can induce inverse Doppler effects" A localized wave packed assembled from many plane waves can still be assigned a (four)momentum at each point. The four components of this momentum are the phase change rates in t,x,y and z given by the imaginary part of the first order derivatives in t,x,y and z. If you apply these first order derivatives on a plane wave then they'll give you the temporal and spatial frequencies of the de Broglie field. The de Broglie wavelength is simply the reciprocal of the spatial frequency. Realizing that the lag of the clock characterized oscillations inside the particle, he associated them with vibrations of the same frequency, but covering the whole space. And he showed that if an observer sees a particle in motion, then these spatial vibrations will seem to him waves propagating faster than a particle...

De Broglie Law of Phase Harmony as the Blue Light Beat Box of the Universe

Frequency is blue light from the future that moves backwards in time as an amplified subharmonic or 1/2 spin energy..."The inverse Doppler effect where an observer measures a higher frequency from a source moving away, is such an intriguing phenomenon that it has attracted substantial theoretical and experimental attention since it was first proposed... ...the energy-momentum flux will be larger in the blue shifted part than in the red shifted part....In a moving frame, they diverge: the mean internal frequency of the photon will increase; simultaneously the orbital frequency of the photon will decrease due to the relativistic law of the slowing down of clocks. Despite the difference in frequency, at any point in space-time these two oscillations must be in phase....This provides a possible physical origin for the postulated law of the "harmony of the phases" first proposed by de Broglie, which lies at the origin of quantum mechanics. ...In a head-on collision between two photons, the interaction will be essentially between the blue-shifted regions which are converging....This state may then decay back into two photons or into an electron-positron pair. Is the electron a photon with toroidal topology? J.G. Williamson and M.B. van der Mark, 1997" Realizing that the lag of the clock characterized oscillations inside the particle, he associated them with vibrations of the same frequency, but covering the whole space. And he showed that if an observer sees a particle in motion, then these spatial vibrations will seem to him waves propagating faster than a particle...

De Broglie-Einstein Law of Phase Harmony from meditation

Internal frequency during meditation is increased (blue light) while external time slows down (gets bigger) as an OM subharmonic sound of the Universe; External time speeds up (as seen by) others while their frequencies (as momentum) are decreased (to red light) in relation to meditation: Thereby maintain a constant phase coherence that is eternal Realizing that the lag of the clock characterized oscillations inside the particle, he associated them with vibrations of the same frequency, but covering the whole space. And he showed that if an observer sees a particle in motion, then these spatial vibrations will seem to him waves propagating faster than a particle...So Heisenberg Uncertainty of position and momentum is transferred into a symmetric mass measurement of particles - but what is covered up is that the position-momentum uncertainty started out, as de Broglie first discovered, with frequency as directly proportional to momentum! So that the "negative frequency" is reverse time as supermomentum or virtual photon energy-information from the future. As we recall from de Broglie: frequency is to time as momentum is to wavelength. So by relying on the wave function as amplitude squared from the wavelength then we are losing the de Broglie supermomentum as reverse time or negative frequency. As we look into a black hole, due to relativity, as the particle approaches the speed of light then the wavelength increases and time slows down. But the internal frequency, as de Broglie realized, based on quantum energy ALSO increases since the mass is due to noncommutative time-frequency (momentum). So the wavelength expands and gets bigger as the frequency of the particle as velocity increases towards the speed of light - due to relativity. But due to the music harmonics of frequency as inverse to time then since the frequency as momentum is increasing (from de Broglie) therefore if the time as wavelength is also increasing from relativity then there HAS to be a negative frequency from the future that has a reverse time. That way the quantum frequency as negative energy (virtual photons) is inverse to the negative time as EMPTINESS from the future. It is William Tiller (working indirectly with Chunyi Lin via Dr. Nisha Manek) that emphasizes the power of Yuan Qi is not from the frequency being negative as virtual photons but from the Negative TIME as negative mass! What both Alain Connes and Basil J. Hiley are emphasizing is that at each "zero point" of space there already is a 5th dimension of noncommutative time-frequency energy with the past and future overlapping. Nobel physicist Gerard 't Hooft agrees: The energy of light is due to it having a "negative refractive index" of spacetime at each zero point of space. So even though light has a zero rest mass the light is CREATING a positive mass as particles due to our own brain physical matter creating a positive refractive index that slows down the speed of light in our measurement perceptions. As Astro-physicist Paul S. Wesson realized - reality is a 5th dimension black hole such that everything is happening at the SAME time at the speed of light. So there is a definite energy to the Universe that is from the future - negentropy - and thus creates the illusion of matter due to light self-annihilating at the zero point of space. This is why H.W.L. Poonjaji and the nondualists of Advaita insist that NOTHING ever HAPPENS and that the SELF is NOT the light but rather the Shakti energy that creates the light - the OM of the light.

When Doves Cry! New Holy Shiitake Qi-infused meditation mushroom exclusive option donation!

Mushrooms are the Fruit of quantum entanglement Biophoton energy.

Therefore in response to the accusations that I am a fraud - I will now offer a NEW EcoEcho Forest cultivation Emptiness Energy Ecology option - Qi-infused shiitake mushrooms:

Holy Shiitake!

You can make a donation - with no guarantees - and for those for whom money is simply an "empty signifier" - of $200 - and I will personally sit in full lotus next to your air and solar drying quarter-pound of forest cultivated Shiitake mushrooms. So as the mushrooms are drying, my full lotus third eye Shen-Qi energy will infuse with the mushrooms themselves (with no physical contact of course).

http://paypal.me/ecoechocultivation

Feel free to email me at ecoechocultivation @ g m ai l . c o om

if you are interested in this exclusive special offer of Qi-infused solar - air - dried shiitake Forest Ecology Emptiness Energy cultivated meditation mushrooms.

As my state musician stated:

When Doves Cry, then the mushroom fruit rains purple.

Goethe's "The Living-Unit of Sound" is noncommutative phase secret of alchemy

Goethe's Tone-Monad as Gurdjieff alchemy: "a contraction towards an inaudible infinite centre. We could also say that this polarity constitutes the light and darkness of the tone. Insofar as all of the undertones and overtones themselves also have their own overtones and undertones, each tone becomes a monad, i.e. a concentration or fold of the web of interwoven expansion and contraction. The audible tone is thus a product of the two forces of contraction and expansion, systole and diastole. Each tone breathes in and out and is a living audible manifestation of an inaudible force-field. This virtual field of vibration or movement weaves an infinite web of expansion and contraction"

Louis de Broglie Law of Phase Harmony visualized

From the invariance of light as the observer, a superluminal phase wave guides, from the future, the space ship (our brains): the Law of Phase Harmony of relativistic quantum 5th Dimension force. Quantum physicist Dr. Guenter Nimtz sends superluminal sound signals through the 5th dimension: ."the superluminal acoustic effect we have described is likely a ubiquitous but imperceptible phenomenon in the everyday world." Physics Professor Manfred Euler: "Binaural hearing is the acoustic analog of the interferometer or double-slit experiments. The two ears can be regarded as an acoustic interferometer, which recovers the phase difference of signals between the two ears by binaural correlation….matter waves are locally in phase with the superluminal particle clocks (de Broglie’s Law of Phase Harmony). The clock runs forever so it’s self-sustaining (consciousness-energy). It resonates with the quantum vacuum....Yet an acoustical answer can be given! Play the above mentioned infinitely rising tune and listen to a parable of scientific progress: The progress goes on but the central epistemological questions remain invariant."

The 5th Dimension is now being utilized as spin chirality of light, the hidden momentum

"Spin resonance was found to occur when the base oscillatory frequency was twice the value of the coupled frequency." This is the secret of the T'ai Chi as the Hempel Effect - 1 plus 1 does not equal 2 in noncommutative phase harmonics. The third harmonic is noncommutative to the root 1 and 2 octave. "An underlying curved space-time provides a distinct contribution to a chiral imbalance, an effect known as the mixed axial–gravitational anomal....We also show, for the first time, how to measure the magnetic spin density of light,...Black hole elasticity and gapped transverse phonons in holography" Nobel Physicist Yang: ."An electrically charged particle is affected by an electromagnetic potential (V, A), despite being confined to a region in which both the magnetic field B and electric field E are zero. If the electric charge through gauge invariance creates an electromagnetic field, wouldn't this isotopic spin also generate a field? And that is the motivation.." Nobel Laureate physicist CN Yang A single photon has such little momentum transfer so then it is amplified through a mirror feedback at the same frequency. Since sound waves are just 1 dimension, so this makes the transduction easier. The entanglement through beam splitting of the mechanical resonator enables frequency transduction while maintaining phase coherence. Total Reflection can approach Unity if Pitch is Half the Wavelength [octave], close to the qubit transition frequency [noncommutative phase]

Jing to Qi is nonlinear harmonics resonance

Raising the body temperature is synonymous with an increased immune response. Professor Abo from Japan confirmed a 40% improvement in the function of the immune system by raising the body temperature by only 1.8° Fahrenheit. Another scientist, Ishihara Yumi, PhD (Japan), established that our immune system much stronger when the body temperature is increased by 1.8°; inversely, the immune system is weakened by 30% if the body temperature is lowered by 1.8°. His statistical analyses revealed a decline in body temperature amongst the Japanese population by an average of 0.9° over the last 50 years. In his studies, Professor Hiromi Shinya, PhD (Albert Einstein College of Medicine, NY, USA) confirmed that, lowering the body temperature by only 0.9°, results in a 30% decline in enzyme and immune activity. He also discovered that cancer cells can multiply much faster at 95°F than at 98.6°F

Eddie Oshins discovers secret of non-western shamanism as quantum noncommutative phase

Nega-particles as reverse time (anti-gravity) guide light as noncommutative energy-information

The Ether-Aether-Emptiness has been Empirically Proven: Yakir Aharonov: "There is a non-local exchange that depends on the modular variable....I'm saying that I have now an intuitive picture to understand interference by saying that when a particle moves through two slits, it always goes through one slit or the other, but it knows which other slit, the slit through which it did not go, whether it is open or not, because there are nonlocal equations of motion." Finally making sense of the double-slit experiment (2017, Aharonov): The nonlocal equations of motion in the Heisenberg picture thus allow us to consider a particle going through only one of the slits, but it nevertheless has nonlocal information regarding the other slit.... The Heisenberg picture, however, offers a different explanation for the loss of interference that is not in the language of collapse: if one of the slits is closed by the experimenter, a nonlocal exchange of modular momentum with the particle occurs....Alternatively, in the Heisenberg picture, the particle has both a definite location and a nonlocal modular momentum that can “sense” the presence of the other slit and therefore, create interference...""What is the effect of this nonlocal motion?...The idea is the following then...In the beginning I certainly don't know through which slit the particle is going because I want to know the module momentum. Then I wait for the interference pattern to happen and after it happens I can check whether the particle was coming from this side [slit] or coming from that side [slit] by a future experiment." "So if I'm able to describe the situation in the present by two vectors: one coming from the future that will tell me through which path the particle went and one coming from the past that tells me that the modular momentum is definite. Then I can see, indeed, there's nonlocal phenomena and not violating causality, because I said I know only from the future through which path the particle went. This is the basic idea and now I will try to describe it more mathematically." as John Bell states: "Is it not clear from the diffraction and interference patterns, that the motion of the particle is directed by the wave?" Grant Sanderson, math/science Stanford: Unlike the doppler radar case where the ambiguity arose because waves were being used to measure an object with a definite distance and speed; what we're seeing here is the particle IS the wave - so the spread out over space and over momentum is not some artifact of imperfect measurement techniques; It's a spread fundamental to what the particle is: analogous to how a musical note being spread out over time is fundamental to what it even means to be a musical note. Grant Sanderson, Math/science degree, Stanford University

Astrophysicist Paul S. Wesson figured out the Law of Phase Harmony explained spiritual phenomenon

Professor Paul S. Wesson realized, the 4D spacetime universe exists in a holographic 5D black hole. Wesson:

...the presence of oscillations in the vacuum have the same properties as de Broglie waves....5D field equations which in 4D has the properties of a de Broglie wave....the difference can show up as a small perturbation which leads to an effect similar to quantum uncertainty...

a "wavicle" is two simultaneous realizations of flat space, one with waves and one without.

From the viewpoint of 5D field theory, waves of de Broglie type have to be considered real.So in 5D all particles behave like photons and everything in the universe is in causal contact with everything else.

an oscillatory phase, which might (if a person is so inclined) be identified with... spiritual modes of existence...separation
between points is zero, so all of the events in the world are in (5D) causal contact. In other words, everything is occurring simultaneously. There is no plausible way to avoid the conclusion that particles which can be seen moving at speeds less than c should be accompanied by waves which cannot be seen and are moving at speeds greater than c.

de Broglie waves are better understood in 5D ...characteristic of inflationary cosmology...its 5D complex generalization...as a model for de Broglie waves. A null interval admits, in a formal sense, velocities in 3D which exceed lightspeed.

a particle not as a point but a tiny ball of trapped waves. ..some of it verging on the mystical.De Broglie waves follow automatically when the expressions for the energy of a particle [E=mc squared] and a wave [E=Planck's Constant multipled by frequency] are combined.

This, admittedly, sounds strange.

Whether one believes in a model like this that straddles physics and spirituality is up to the individual....However it is remarkable that such a model can even be formulated, bridging as it does realms of experience which traditionally have been viewed as immutably separate.

"We were simply studying these circuits for the purpose of developing an amplifier, which we did," says researcher Sorin Paraoanu, a theoretical physicist at Aalto University. "But then we asked ourselves—what if there is no signal to amplify? What happens if the vacuum is the signal?"
https://www.scientificamerican.com/article/something-from-nothing-vacuum-can-yield-flashes-of-light/

Also, a simple connection between Q_M and relativity theory for the De Broglie particle/pilot wave concept shows that v_p v_w = c² is required, where the subscripts p and w refer to particle and wave, respectively. Thus, since v_p < c, always, via relativity theory, v_w> c always for the information wave components making up the De Broglie pilot wave.

http://www.entelechyjournal.com/httpdocs/billtiller.htm

"When high energy substances of the subconscious mind emerges, they should be one's guiding force."
qigong master Yan Xin

The Hempel Effect

Visually, the frequency and amplitude changes but the EAR hears no difference - both phases are the Perfect Fifth just inverted as undivided yin-yang (the Taiji). I was discussing noncommutative phase with Nobel physicist Brian Josephson - and he said that I didn't understand how octaves were a geometric logarithm - so that C to G is 3/2 yet G to C is 3/4 as the harmonic series. So I tried to point out to him that since the 2 and 4 are the SAME C as "pitch" - then in the same octave, when doubled back, you can not HAVE the same G as Both the Perfect Fifth and Perfect Fourth. Why? Because 3/4 is the reverse direction in time - so that now the "3" is the denominator as a new root tonic. And so the harmonic series assumes this is a logarithmic equation as a ratio that can be inverted - but you can not evenly divide the octave and the Perfect Fifth since 2 does not go into 3 evenly. So this means that 3/4 is actually C to F while C to G is 3/2 and the C to F was derived from doubling 2/3. So this is called the "phantom tonic" in music theory and reveals the noncommutative phase origin of the music harmonics - as Alain Connes recognizes. Let us draw up a fundamental vibration with its first and second harmonic overtones [1:2 and 2:3]….if we then shift the phase relationship, we get a totally different course of the combined curve; that is, of the pressure course [amplitude and frequency] which is apparently effective in the final analysis. When looking at both curves, one might suppose that in the two cases we should hear two sounds that are just as different. But in fact our ear does not notice any difference. biophysicist Vitus B. Dröscher states in his book, Magic of the Senses, p. 168 I defer to Cambridge University physicist R D Patterson who, in his classic academic “Psychology of Music” journal paper on the spiral pulse-stream processor—describes how period is inverse to pitch and natural integars for pitch create a free-energy transduction from the ear (sound-wave-mechanical pressure, water pressure-electromechinical transduction) to the brain. Normally period is measured in frequency—as is the case with the photoelectric effect—but since period is the inverse of pitch then the natural number integars of frequency as period can be translated back to Pythagorean Just Tuning as the Natural integar numbers of Infinite Quantum Potential. However, because the human ear is not sensitive to the phase of a sound, only its amplitude or intensity, only the magnitude of the envelope is heard. Therefore, subjectively, the frequency of the envelope seems to have twice the frequency

Philolaus relied on noncommutative phase, same as Daoist alchemy harmonics

Philolaus relied on noncommutative phase, same as Daoist alchemy harmonics, 4/3 (yin, C to F harmonic) within 3/2 Yang (C to G overtone) as Yang (3/2) is within yin (4/3) 0 to 8 is the 3/2 frequency (2/3 as C to F subharmonic of 0 to 12 now converted to 6/8 as 3/4 wavelength of 0 to 8 root tonic!) Professor Richard McKirahan: "So instead of taking 12:9, which is 3/4 of 12, we take 8:6, which is 3/4 of 8. And so by adding the length 12 to 8 [as geometric magnitude not wavelength!!] with the length 8 to 6, [as geometric magnitude, not wavelength!!] we get the length 12 to 6, which corresponds to the ratio 2:1." So he states: "beginning at the bottom note...and descending via another (a fifth above the bottom note)." So he says "bottom note" twice to emphasize they are symmetric and then says "via another" to HIDE that the "other" is the OCTAVE!! That is the bait and switch - and then he says - (1, 4) = (7, 5) What is (1, 4)? It is a Perfect Fourth which is the PITCH of C to F (overtone, 4/3). Anyone who actually knows how to play music would not fall for this bait and switch! What is (7, 5)? It is a Perfect Fourth which is the PITCH of C to G! "The term subcontrary may refer to the fact that a tone based on this mean reverses the order of the two fundamental musical intervals in a scale. It is believed that Archytas or one of his contemporaries gave the name "harmonic" to the subcontrary mean because....[book source: Infinite Series cover up of the noncommutative "bait and switch"]. Math professor Luigi Borzacchini: "Boethius’ text that I am going to analyze shows that the early musical theory of incommensurability was somehow known, even though it had been overcome by a sudden rupture." Professor Richard McKirahan: "The word translated epogdoic is not a musical term but a mathematical one. An epogdoic ratio is the ratio of 9 to 8. The occurrence of a mathematical term here is unexpected. It has been treated as an unimportant anomaly but in fact it is the key to the entire fragment....The word magnitude normally refers to physical size, but here it is given a new application, extending the notion of magnitude to include musical intervals." Or as Professor Borzacchini states: " These remarks raise the question of the difference between the ancient Pythagorean ‘musical’ perception as displayed in the Pythagorean idea of ‘linear number’ in Boethius [Philolaus] or in Nicomachus, and the modern ‘geometrical’ perception of the linear numerical magnitudes."

Ancient Advanced Acoustic Alchemy - free training book

Sunday, April 29, 2018

You said that the Daoists only utilised 4/3 (yin) and 3/2 (yang) because together they both add together to create the octave, but did they not make use of other ratios too?

No comments:

Post a Comment