The sign of the underlying phase slope is ambiguous. Because leads by radians (or 1/4 cycle) for positive frequencies and lags by the same amount for negative frequencies, the ambiguity about the phase slope is resolved simply by observing a cosine and sine operator simultaneously and seeing which one leads the other.
https://en.wikipedia.org/wiki/Negative_frequency
Of course this is not allowed in relativity. And yet in quantum nonlocality we have simultaneity that is NOT observable!! How is this paradox resolved? Through logical inference as listening that is superluminal noncommutative phase in quantum biology as alchemical meditation
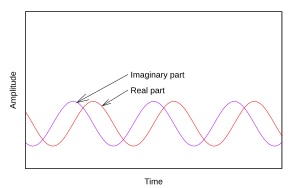 | |
| A negative frequency causes the sin function (violet) to lead the cos (red) by 1/4 cycle. |
So the imaginary phase is what causes a time-reversed quantum potential that is nonlocal. This imaginary phase is inherently asymmetric as math professor Lou Kauffman explains in his "itinerant" algebra of time logic.
The negentropy of the Universe, as Roger Penrose points out, is due to the inherent asymmetric time of the accelerating spacetime. So the origin of the Universe is highly coherent asymmetric time as quantum negentropy creating the gravitational potential as dark energy. This origin of the Universe then is from negative frequency as inverse to asymmetric time that is inherently precognitive protoconsciousness as a negative frequency signal, a discrete nonlocal formless awareness.
When the "sum" is used then the negative frequency is canceled out and negative frequency is thus considered "equivalent" to positive frequency - thus the noncommutative asymmetric time is lost!!
So defining a signal based on power as squaring then covers up the true source of energy from asymmetric time and negative frequency!
This is the fundamental insight that Heisenberg discovered and Fields Medal math professor Alain Connes focuses on - that the "signal" of a photon is inherently asymmetric time as noncommutativity or a noncommutative time-frequency signal that changes based on the order of time it is "observed."
Therefore the imaginary time is inherently an asymmetric time shift that exists as negative frequency whether it is observed or not. It can be logically inferred and indeed LISTENED to in quantum biology as meditation with music listening proven to be up to ten times faster that time-frequency uncertainty.
Because digital signals are almost always randomized before being modulated, the spectrum is flat over its passband. As stated earlier, the average signal level is measured, not the peak level as is the accepted practice in measuring analog video signals. A spectrum analyzer is often used for this measurement, but several corrections in its reading must be made. The biggest is to correct for the occupied bandwidth of the signal, versus the bandwidth over which the measurement is made. The bandwidth over which the signal level is measured (the noise bandwidth) is roughly equal to the resolution bandwidth of the spectrum analyzer. However, the two are not quite the same, and for accurate measurements a correction factor must be used.
Since signal energy is distributed evenly across the band, the power of the signal is proportional to the bandwidth over which the measurement is made.
So it is assumed to be a randomized flat frequency bandwidth as the background for a digital signal. But even an analog signal assumes a symmetric squaring that makes the negative frequency canceled out or ambiguous.
Exponents as reciprocals are noncommutative.
https://www.uncp.edu/sites/default/files/2022-12/Negative%20Exponents.pdf
So in Music we have 2 to the 19th as 3 to the 12th = 3 to the 1/19th as 2 to the 1/12th with a geometric dimension less than any positive number as noncommutative nonlocality with 2/3 as C/F and 3/2 as G/C.
So whether impedance or resistance is used for the power signal then it depends on squaring that hides the negative frequency.
If the signal is represented as a voltage or a current and it is connected to a (1 ohm) resistor, the power dissipated in the resistor is proportional to or .
Energy is used to measure the signal content in a signal of FINITE duration. Power is a measure for a signal that has an INFINITE duration (sine wave etc). The signal must be periodic for this calculation to be possible.
Either way the phase is symmetric and thus asymmetric time and negative frequency are covered up.
this is a measure of the average energy of the signal. Also note that this equation requires a period T. Therefore, the power of a signal is equal to the mean of the amplitude squared within one period.
And this is the error that Planck made when he converted photons to joules! He canceled out the time as a symmetric assumption of a spatial unit - thereby covered up the fact that the Law of Phase Harmony as per de Broglie relies on a negative frequency and time reversed signal (that is not a symmetric spatial wavelength).
The power transferred from one place to another by a wave in any linear medium is also proportional to the square of the amplitude of the wave -- height for water waves, pressure for sound waves, electric and magnetic fields for radio waves, etc.
If you have some kind of signal, the odds are very good that when you translate it into something real, the power will be proportional to the signal amplitude, at least at constant frequency.
And so "period" is inherently a symmetric irrational magnitude from the wrong music theory!!
Wavelength is an angular frequency function that is also inherently symmetric unless "observable simultaneously"....
treating time and causality as primitive concepts, neither of them being `more primitive' than the other. The decision regarding which concepts to assume as primitive and which statements to regard as axioms depends on the choice of the angle at which we contemplate the whole. This standard approach is based on the presupposition that the concept of a point-like particle is a viable approximation. However, this assumption is not supported by a realistic approach to doing physics and, in particular, by quantum theory.... This is impossible without taking into account the relative frequencies and correlations observed in relevant experiments.
https://arxiv.org/pdf/2202.07302.pdf
Charge originates from noncommutative spin!
http://article.sapub.org/10.5923.j.ijtmp.20160604.03.html#Sec7
The primitive spectrum of a ring is a non-commutative analog of the prime spectrum of a commutative ring
A major difference between rings which are and are not commutative is the necessity to separately consider right ideals and left ideals. It is common for noncommutative ring theorists to enforce a condition on one of these types of ideals while not requiring it to hold for the opposite side.
a primitive ideal is the kernel of a non-zero irreducible *-representation.
It turns out that for a C*-algebra A, an ideal is algebraically primitive if and only if it is primitive in the sense defined above. Theorem. Let A be a C*-algebra. Any algebraically irreducible representation of A on a complex vector space is algebraically equivalent to a topologically irreducible *-representation on a Hilbert space.
The outcome is that the space of primes could be seen coming out of a noncommutative space that was extremely natural. When you have an absorption line, it’s a single line, so normally it would not be seen. Unless the line had some thickness, some width, you would not see it. Mathematically speaking, the zeros of zeta don’t have a thickness. You have to artificially make them a little bit thick in order to be able to see them. And that’s very hard. It is exactly this technical point that is now being treated much better but that took enormous time to understand. ...If noncommutative geometry were just dealing with very strange spaces, I don’t think it would be very convincing to people. But for two fundamental spaces — for spacetime, the space where we live, and for the space of primes — it can bring something new and embody the intuition behind them.
the integers, the real numbers, the spaces you are used to working with — all of these things will actually depend on a parameter that is in the backstage. What is in the backstage will govern a randomness that will be inherited by the usual characters of mathematics that you are working with.
This is a fantastic idea. Technically speaking, what does it mean? Instead of looking at the space, you look at what are called the sheaves of sets over the space. Then when you do set theory, you can do any mathematics you want, you can look at sheaves of groups or sheaves of topological spaces. You can recover the space and its topology, which is in the backstage, just by looking at set theory “with parameter”. What is a point of the space? A point of the space is a way to suppress the randomness in the events that are occurring on the stage. Then when you use a point to look at what is going on on the stage, it is as if it is no longer random.
What I find incredibly revealing, is that when you compute the points of a topos, even of a very simple topos, you get in general a noncommutative space!
[According to Cartier, Grothendieck believed that the speed of light had been corrupted by the devil.]
I never met Grothendieck, but I think that I know him so well, from his writings. In several of them, he complains that people don’t understand what a topos is. It shows how common it is that mathematicians say “This is not mathematics”, or “This is not serious”, just because they don’t understand. He suffered a lot from that. The concept of topos is an amazing discovery that gives a completely new way of thinking about mathematics.
if one takes a spectral point of view of geometry, then there is a natural manner of defining what is called in physics an “action”, for that geometry. This will measure how suitable the geometry is. This action turned out to be spectral and depends only upon the line element, upon its spectrum....
Some people have tried for instance to obtain gravity from gauge fields, but what I am saying is quite different. What I am saying is that once you introduce some fine structure in the geometry of spacetime, then pure gravity will give you not only the ordinary gravitational force, but also the other forces of nature, which are the electroweak and the strong force. So it’s not a unification from gauge fields, but it’s a unification from gravity.
Why is it natural to view a space spectrally and to define the action from a spectral invariant?
the new standpoint that I had defined, which is spectral, is exactly parallel to the shift that occurred in physics between the definition of the unit of length by means of the platinum bar, and the definition by means of comparison with wavelengths of a fixed chemical.
The formula for distance in noncommutative geometry will use the fact that the line element does not commute with the coordinates in the space.
The reason time is passing, and passing in a way that we don’t control at all, is precisely the lack of reproducibility of the quantum.
"Lee [Smolin] and I discussed these paradoxes at great length for many months, starting in January 2001. We would meet in cafés in South Kensington or Holland Park to mull over the problem. THE ROOT OF ALL THE EVIL WAS CLEARLY SPECIAL RELATIVITY. All these paradoxes resulted from well known effects such as length contraction, time dilation, or E=mc^2, all basic predictions of special relativity."
Joao Magueijo, Faster Than the Speed of Light, p. 250
Albert Einstein (1954):
"I consider it entirely possible that physics cannot be based upon the field concept, that is on continuous structures. Then nothing will remain of my whole castle in the air, including the theory of gravitation, but also nothing of the rest of contemporary physics."
John Stachel, Einstein from 'B' to 'Z', p. 151"
the definition of a circle: all the points that are equidistant from a given point. The definition impressed him with “its simplicity and clarity,” he wrote years later. The property of perfect rotundity had until then appeared to him to be “mysterious beyond words.”
A tremendous, demanding, tumultuous friendship was struck up. “Sometimes he was so nice. Other times, we would knock on his door and he would slam it in our faces, or he would tell us that we were messengers of Satan,” Schneps said. She recalled that, if a leaf broke off a plant in his home, he would place the fallen leaf in its own glass of water. He told Schneps and Lochak that he and the plants could communicate. “I think he was very lonely,” she said. He was preoccupied with the problem of evil and felt that, when people set aside what they were doing and focussed on this, the evil would end. “I don’t think he was crazy,” she said. “Look at us chatting away here, with everything going on in Ukraine.” It was the end of February. “He would say that we are the ones who are crazy.” She and Lochak attempted to visit him each year. At times, he would gather a basket of apples from his yard to give to them; at other times, he would accuse them of trampling on him. He never spoke with them about mathematics.
https://phys.org/news/2023-09-hermit-eccentric-french-math-genius.html
It's very simple, negative frequency just means clockwise rotations (or just rotations in the opposite of your convention)...Negative frequency is a property of complex exponentials that have imaginary exponents (what I call 'spinning numbers').
https://arxiv.org/pdf/physics/9712022.pdf
The characterization of non-stationary signals requires joint time
and frequency information. However, time (t) and frequency (ω) being
non-commuting variables, there cannot be a joint probability density
in the (t, ω) plane and the time-frequency distributions, that have been
proposed, have difficult interpretation problems arising from negative
or complex values and spurious components.
Franz Luef: Noncommutative geometry and time-frequency analysis
https://iopscience.iop.org/article/10.1088/1742-6596/284/1/012003/pdf
Shahn Majid on the noncommutative black hole and negative frequencies
Events can be separated in many directions in space, but if two events are separated by time, then one event must precede the other, and all observers will agree on this. General relativity does not address the nature of time for extremely small intervals where quantum mechanics holds. In quantum mechanics, time is treated as a universal and absolute parameter, differing from general relativity's notion of independent clocks. Reconciling these two theories is known as the problem of time. As of 2023, there is no generally accepted theory of quantum general relativity.[18]
We can’t communicate using phase velocity speed according to standard science.
The reason time is passing, and passing in a way that we don’t control at all, is precisely the lack of reproducibility of the quantum.




No comments:
Post a Comment