Lendvai, Ernő (1971). Béla Bartók: An Analysis of his Music. introd. by Alan Bush. London: Kahn & Averill.
So this book was key to my master's thesis but I never explained the key point I was making from the book.
OK supposedly most people hear this "wrong" - the Tritone Paradox
Shepard predicted that the two tones would constitute a bistable figure, the auditory equivalent of the Necker cube, that could be heard ascending or descending, but never both at the same time. Diana Deutsch later found that perception of which tone was higher depended on the absolute frequencies involved: an individual will usually find the same tone to be higher, and this is determined by the tones' absolute pitches. This is consistently done by a large portion of the population, despite the fact that responding to different tones in different ways must involve the ability to hear absolute pitch, which was thought to be extremely rare. This finding has been used to argue that latent absolute-pitch ability is present in a large proportion of the population.
So these music perception scientists do not realize they are talking about Noncommutative phase! Let's redefine it this way:
Each Shepard tone consists of a set of octave-related sinusoids, whose amplitudes are scaled by a fixed bell-shaped spectral envelope based on a log frequency scale. For example, one tone might consist of a sinusoid at 440 Hz, accompanied by sinusoid at the higher octaves (880 Hz, 1760 Hz, etc.) and lower octaves (220 Hz, 110 Hz, etc.). The other tone might consist of a 311 Hz sinusoid, again accompanied by higher and lower octaves (622 Hz, 155.5 Hz, etc.). The amplitudes of the sinusoids of both complexes are determined by the same fixed-amplitude envelope—for example, the envelope might be centered at 370 Hz and span a six-octave range.
Shepard tones consist of octave-spaced components, whose amplitudes are generated under a fixed bell-shaped spectral envelope. They are well defined in pitch chroma, but generate octave confusions that in turn can produce ambiguities in the perceived relative pitch heights when their chromas are exactly a tritone apart (the tritone paradox).
So the "paradox of the poles" as I discuss in my master's thesis, as per Edward Rothstein and Erno Lendvai - is also the basis for the "Tritone Substitution" in jazz music.
https://musicintervaltheory.academy/learn-how-to-write-music/tritone-substitution/
So the idea here is that our ear is reaction to the overtone series of the Tritone so that it is a substitute for the root tonic in the bass note.
So it turns out that John Coltrane's musical secret described by Stephon Alexander in the "Jazz of Physics" book - as a "circle" of pentatonic fifths - is actually due to this Tritone Substitution as the "paradox of the poles" that Erno Lendvai called the asymmetric tonal acoustics system.
https://www.nicktomalin.co.uk/single-post/2015/04/08/some-applications-of-the-axis-system
So he goes into how Coltrane chord progressions are best explained by the "axis" system of Erno Lendvai.
(tonality can after all only be supported by means of the asymmetrical division of the tonal system; in the case of a division based on equidistance, it is not possible to know which note to keep to).
http://www.mi.sanu.ac.rs/vismath/lend/b6.htm
So that phrase perfectly explains the Tritone Paradox but ALSO the Tritone Substitution technique in jazz.
In terms of Tritone Substitution as per John Coltrane we are referring to the asymmetrical tonal overtones that are in common between the root tonic and the tritone - as the "paradox of the poles."
In terms of the Tritone Paradox we are referring to the inability to distinguish the root tonic and thus the proper absolute pitch based on the sequence of tritone intervals listened to.
So as I emphasized in my Master's Thesis - to resolve the crisis of materialistic Western metaphysics there has to be a dialectical reversal via the infinite Absolute Void as the "beats of no beats." So that if the root tonic is no beats then the Tritone as the square root of two is only resolved by its own overtone harmonics. And so the root tonic being defined by its overtones of the octave and Perfect Fifth are only able to include the Perfect Fourth based on the Tritone Paradox of no longer being able to tell the DIRECTION of time as absolute pitch.
So I give another quote in my Master's Thesis from Martin Gardner about how if the amplitude is changed - or volume - this can correct the change in frequency due to the Doppler shift of changing the speed. So similarly with the Tritone Paradox - the amplitude is being shifted between the octave equivalents in pitch as the tritone is played - and thereby shifting the perceived direction of the pitch change due to a change in the perceived overtones of the tritone interval.
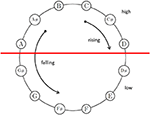
Figure 2. Shepard tones arranged in the pitch-class circle. Tritone paradox: Shepard tones in the upper half (A, A#, B, C, C#, D) are judged as higher than those of the lower half (D#, E, F, F#, G, G#). Proximity principle: When the distance between two pitch classes is clockwise shorter than counter-clockwise, participants prefer rising judgments; in the opposite condition, participants prefer falling judgments.
Again this PROVES that people listen based on absolute pitch over relative pitch. Amazing. So this is noncommutative phase in action.
Dr. Stephon Alexander just had this book published which corroborates my qigong music analysis of alchemy.
The Jazz of Physics: The Secret Link Between Music and the Structure of the Universe
pp. 223-4, The Jazz of Physics
That
is the Infinite Spiral of Fifths!! The perfect fifths from natural
sources is the infinite spiral of fifths which is most closely
approximated in Western tuning by the "sixty cycle" circle of fifths.
So the author is extrapolating to the secret meaning of Coltrane's connection to Einstein:
Tritone Paradox - Diana Deutsch pdf
interesting.
That's really wild.
So the left brain as talking is overriding the right brain as absolute frequency perception!!
Deutsch, D., Henthorn T. and Dolson, M. Speech patterns heard early in life influence later perception of the tritone paradox. Music Perception, 21:357–372, 2004.
very bizarre!!
Particularly, Repp (1997) revealed that the subjectively highest Shepard tones were shifted about six semitones from their envelope center. Repp goes on to say that some listener's judgments are swayed by envelope effects whereas others rely more on pitch class. Interestingly, there is an analogous situation for vowel boundary perception where the positioning of harmonics relative to a fixed formant frequency envelope can change sharply as a function of the fundamental frequency (e.g., Hirahara, 1993; Hirahara et al., 1996).
very fascinating indeed!!
virtual pitches do not necessarily (e.g., missing-fundamental tones). For Shepard tones, the most salient virtual pitches correspond to one of the partials (Terhardt et al., 1982b, 1986). Terhardt (1991) suggested that when such virtual pitches form a rising pair, the tritone pair is judged as rising, whereas when they form a falling pair, the tritone pair is judged as falling. Furthermore, virtual pitch salience is determined by, among other factors, the salience of spectral pitches, which depends on the spectral weighting function. This function reaches its maximum at a specific frequency region, the preference region. Terhardt postulated that individual differences in the tritone paradox are possibly due to individual variability in spectral weighting functions. The predictions of VPT for Shepard tones were confirmed by Terhardt et al. (1986) and Repp and Thompson (2010).
So this brings us back to the Tritone Substitution model based on the common "virtual pitches" or overtones!
units in the primary auditory cortex respond more consistently to frequency-modulated tones than to steady tones and that some units are tuned to upward and others to downward frequency shifts
The contrastive aftereffect revealed in the present study could also be interpreted as the context effects revealed by several studies (Repp, 1997; Giangrande et al., 2003; Englitz et al., 2013; Chambers and Pressnitzer, 2014; Chambers et al., 2017). Repp (1997) found that the principle of proximity is not restricted to tone pairs, but also applies to triplets. Specifically, participants have judged the tritone pair C − F# more often as rising when it was preceded by the Shepard tone D# (3 semitones clockwise or 9 semitones counter-clockwise with respect to the first tone). When it was preceded by A (9 semitones clockwise or 3 semitones counter-clockwise with respect to the first tone), the reversed pattern occurred. Repp explained this result by the fact that in both cases the total range was kept to 6 semitones. More recent studies have revealed context effects caused by preceding tone sequences (Englitz et al., 2013; Chambers and Pressnitzer, 2014; Chambers et al., 2017). Preceding tones have caused upward biases when they have been shifted less than 6 semitones from the first tone (clockwise). Preceding tones have led to downward biases when they have been shifted more than 6 semitones from the first tone. In the present study, the 7-note short adaptor sequences before each tritone pair might have served as contextual upward or downward bias.
To discuss this point, we consider the consistent condition C6 − C6 more closely because of the pronounced contrastive aftereffects. The short version of the rising C6 sequence comprised the Shepard tones C, C#, D, D#, E, F, F#, and G. Possibly, these tones (except for C) caused an upward bias for the tone pair C# − G because the clockwise distances the sequence tones were shifted from the first Shepard tone were shorter than the counter-clockwise distances. In contrast, the sequence tones caused a downward bias for the tone pair G-C#, because the reverse pattern occurred. Thus, the prior context would cause fewer lower responses in C# − G and would cause more lower responses in G − C#. Actually, there were more lower responses for G − C#, but not fewer lower responses in C# − G in the study data. Thus, the response pattern for the rising C6 adaptor sequence cannot be explained by assuming that only the prior context was active. Thus, possibly, adaptation and context effects were active. For this, the effects would add up in G − C# and would cancel each other in C# − G, which is in accord with the study data.

No comments:
Post a Comment