every point in the Penrose diagram corresponds to a 2-dimensional sphere .
Purely astigmatic lens is completely positive in one direction and negative in the other direction. And the curvature due to pure gravity is of that kind. So I could understand how the focusing of light rays behaved - from having this experience of doing physics at school. So that was useful to me...
So there not lenses now - a kind of lens that gravity - how it acts on light rays. And the purely positive focusing lens - convex lens which is positive focusing is what matter does.
Sir Roger Penrose
https://www.einstein-online.info/en/spotlight/the-singularity-theorem/
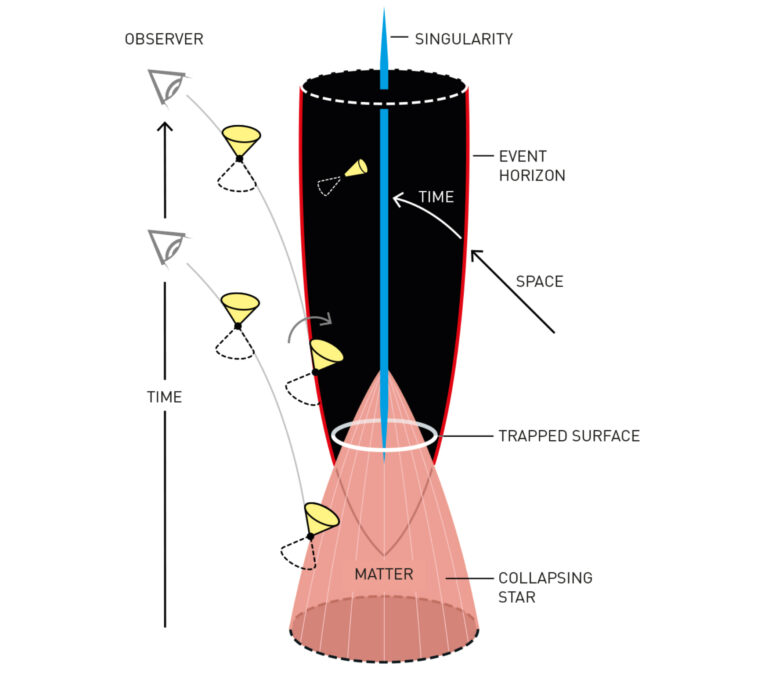
As the matter falls inwards, you surround it, probably in the vacuum region, outside the matter as it collapses in, you can draw a sphere around it. It has this curious property that if you have an instantaneous flash of light on this sphere, that the light rays converge BOTH ways. On the convex.. on the concave side the light rays will converge and on the convex side the light rays will diverge. On this convergence on both sides is nothing wrong if it is locally but if it goes all the way around the sphere then I call this a Trapped Surface.
If you looked at the Future of that Region then you had a boundary that was compact - it closed in on itself and that was inconsistent with the initial surface being Non-compact. And I could develop a theorem.
There wouldn't be a universe if they're weren't conscious beings in it because otherwise there would be no one to see it.
Understanding is Consciousness....You follow the Schroedinger Equation and suddenly it JUMPS. That's not following the Schroedringer Equation - that's called the "collapse of the wave function" - we need a theory of the collapse of the wave function....
Quantum computers do not "harness" the collapse of the wave function...I don't want them to claim to be conscious when they're not. That's all.
noncommutative Klein-quartic = taiji=wuji
to create a 3-holed torus by attaching the sides of this surface to each other.
https://math.ucr.edu/home/baez/klein.html
It's a 3-holed torus, but drawn in a way that emphasizes the tetrahedral symmetry lurking in this surface! You can see there are 56 triangles: 2 for each of the tetrahedron's 4 corners, and 8 for each of its 6 edges.
However, 12 is just half of 24, so there should be an extra 2-fold symmetry, besides the 12 rotational symmetries of the tetrahedron. And there is! It consists of twisting Klein's quartic inside out, like this:
More precisely, if you follow the four corners of the tetrahedron, you'll see that two come back to where they were, while the other two get switched. So, this symmetry acts as a reflection, or odd permutation, of the 4 corners. The rotations act as even permutations of the corners.
If you look carefully, you'll see each corner of his tetrahedral gadget is made of a little triangular prism with one triangle facing out and one facing in: for example, the pink triangle staring you right in the face, or the light blue one on top. Since 4 × 2 = 8, there are 8 of these triangles. Abstractly, we can think of these as the 8 corners of a cube! They aren't really, but we can pretend. The way these 8 triangles come in pairs corresponds to how the vertices of a cube come in diagonally opposite pairs.
You see, the cubes in the Klein quartic have an inherent handedness to them. You can go between the 8 triangles of a given cube by following certain driving directions, but these driving directions involve some left and right turns. If you follow the mirror-image driving directions with "left" and "right" switched, you'll get an anticube.
Apart from having the opposite handedness, anticubes are just like cubes
Daoist Master Wang Liping is taught this SAME lesson by his Dragon Gate Daoist alchemy immortal masters - to think of the corner of a room as having two triangles opposite to each other.
Everything then goes through, and out the other side at decelerating speeds to open up the twin universe
https://www.bu.edu/wcp/Papers/Scie/ScieStar.htm
vid of a Klein Bottle made from Two Moebius strips
The surface of a ball is a two dimensional sphere. Imagine a two dimensional entity in that two dimensional surface. It can travel forwards and backwards, or right and left. But it can’t travel up or down because a two dimensional surface has no thickness. And while it is traveling no matter were it travels in the sphere it will never find and edge.
A torus (the surface of a doughnut) is another two dimensional surface that has no edge.
Both of these are two dimensional surfaces that are embedded in three dimensional space.
A Mobius strip is also a two dimensional surface embedded in three dimensional space. However, unlike the sphere or torus it has an edge.
You can think of a Klein bottle as a Mobius strip whose edge has bonded to itself. That is not easy to picture.
It might be easier to think of a Klein bottle in relation to a torus. A torus is a tube whose ends are joined. A Klein bottle is a tube whose ends are joined but first one end passes through the wall of the tube and travels in the tube to meet and join its other end.
In three dimensional space a Klein bottle is a two dimensional surface that passes through itself like a ghost through a wall.
https://www.quora.com/Is-a-Klein-bottle-actually-just-a-3D-version-of-a-mobius-strip



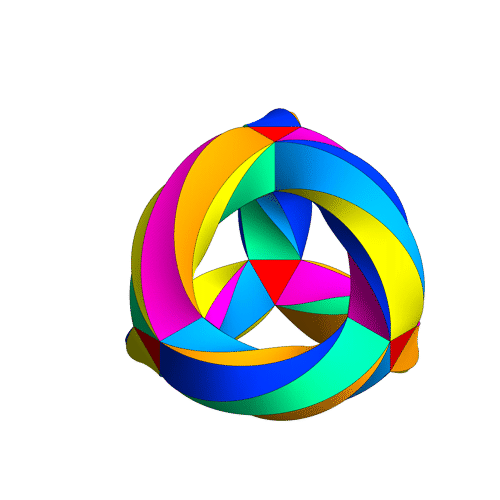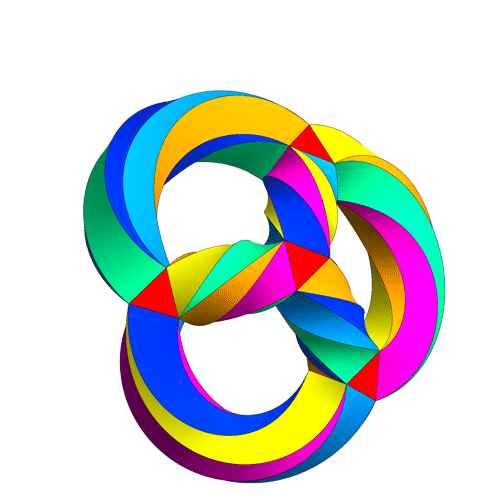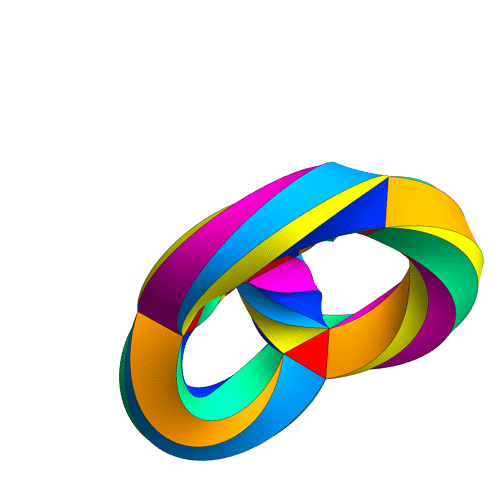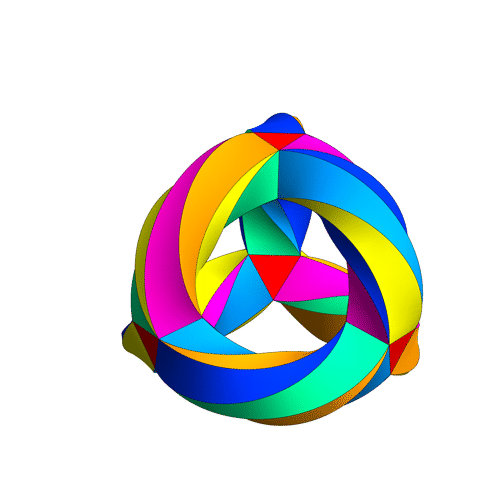

No comments:
Post a Comment