Time Reversal as bidirectional teleportation without any particles - video lecture
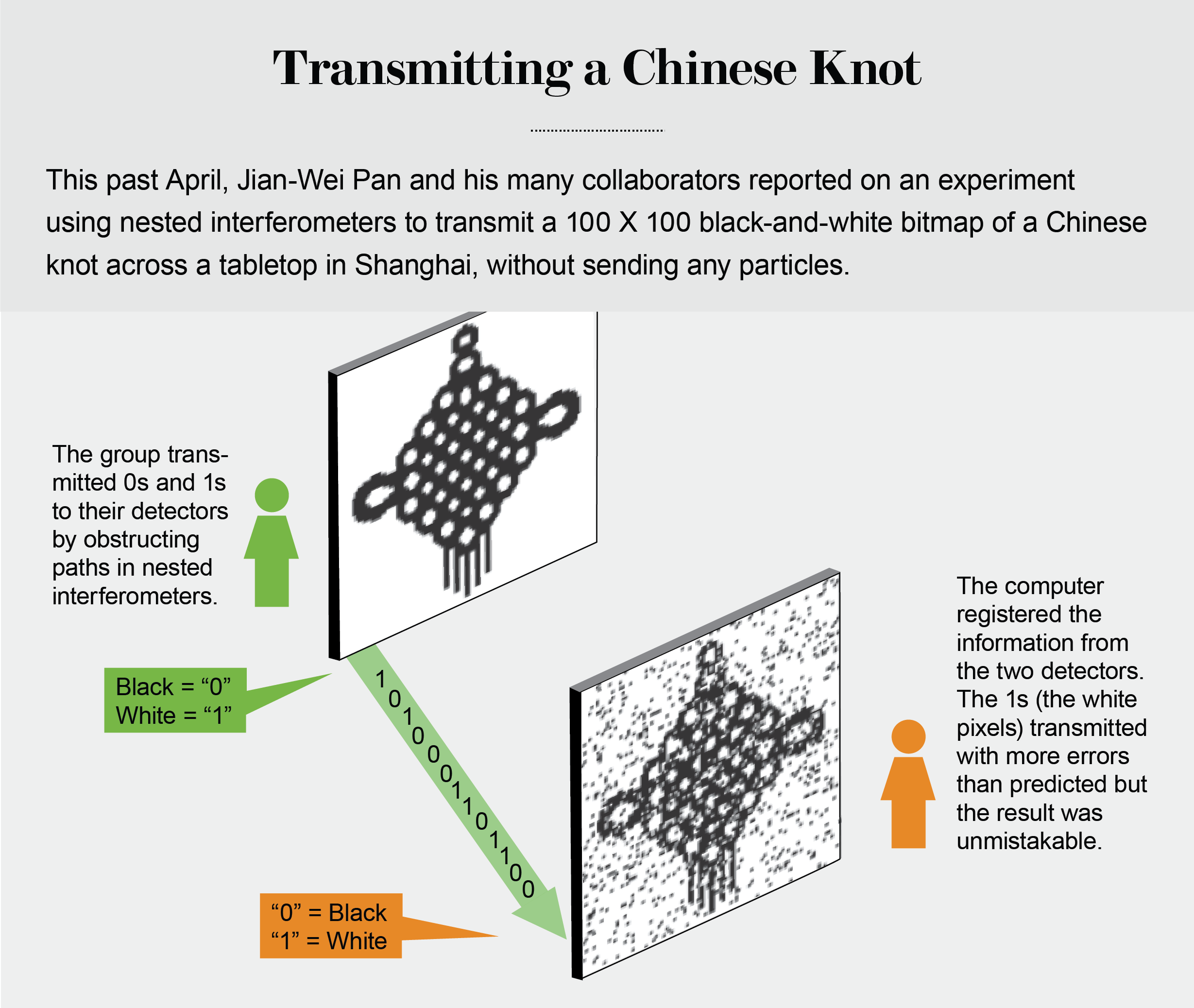
We can transfer a message without particles being present in the transmission channel.
It's feasible. It has been done.
Still Amazing thing! Quantum Teleportation without anything!
Lev Vaidman quote
about 18 minutes into the lecture
In classical mechanics, only the initial state of the system is needed to determine its time evolution. Additional information on the final state is either redundant or inconsistent. In quantum mechanics, however, the initial state does not convey all measurements’ outcomes. Only when augmented with a final quantum state, which can be understood as propagating backwards in time, a richer, more complete picture of quantum reality is portrayed. This time-symmetric view leads to a subtle kind of a local hidden-variables theory, where true collapse never occurs, yet can be effectively observed. Moreover, the Born rule and the borderline between classical and quantum systems can be derived from, respectively, the requirements of stability and “macroscopic robustness under time-reversal.’’ The significant role of macroscopic systems in amplifying and recording quantum outcomes then directly follows. Some possible cosmological consequences of this construction are discussed, especially those related to the breakdown of the “Pigeonhole principle” and on-going work on the concept of “Quantum Holism”.
Eli Cohen: A Final Boundary to the Universe vid
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.91.032116
Taichi in action (science style)
He works with Yakir Aharonov on Nega-Particles using weak measurements (entangled photons)
Some Notes on Counterfactuals in Quantum Mechanics
Forward—and backward—evolving wavefunctions are granted equal causal efficacy. Consequently, effects proceed not only forward in time but may also zigzag back and forth. Hence, what appears to be nonlocal in space becomes local in spacetime. This account is therefore fully physical, i.e., compatible with all predictions of quantum mechanics and all experiments performed until now, independent of philosophical preferences.
So the Weak Measurement is the OVERLAP of the forward and backward "selections"
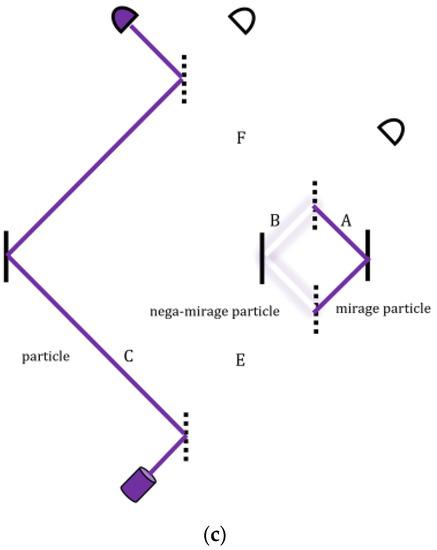
Returning to quantum oblivion, our question becomes sharper. Not only does the electron remain unchanged after the interaction that changed the positron’s momentum, but there are also the two remote detectors which took part in this non-reciprocal interaction—just by remaining silent. If no photon has ever been emitted from the electron–positron pair towards these detectors, located arbitrarily far away, how can their mere non-clicking affect the positron back?
The overlap between the pre- and post-selected states gives rise to an odd trajectory (purple) which harbors a short-lived particle in the middle of the “empty” path.
So if you set up "two shutters" it changes the clicking path....
the “empty” path of the large MZI, where apparently no particle has passed, was traversed by a pair of mirage particles, one with positive and the other with a negative mass. The smaller MZI briefly split them, before they reunited to form the apparent “nothing” again [50].
We can alter the pattern on the screen by inserting a pane of glass in one beam’s path. Glass slows the light, so the peaks and valleys of its waves no longer match those from the other beam. A certain thickness of glass slows one beam just enough so its peaks arrive with the valleys of the other. Different areas of the screen now turn dark, where the light in the two beams interfere with each other destructively. If we were to place a photon detector at such a spot, no light would register.
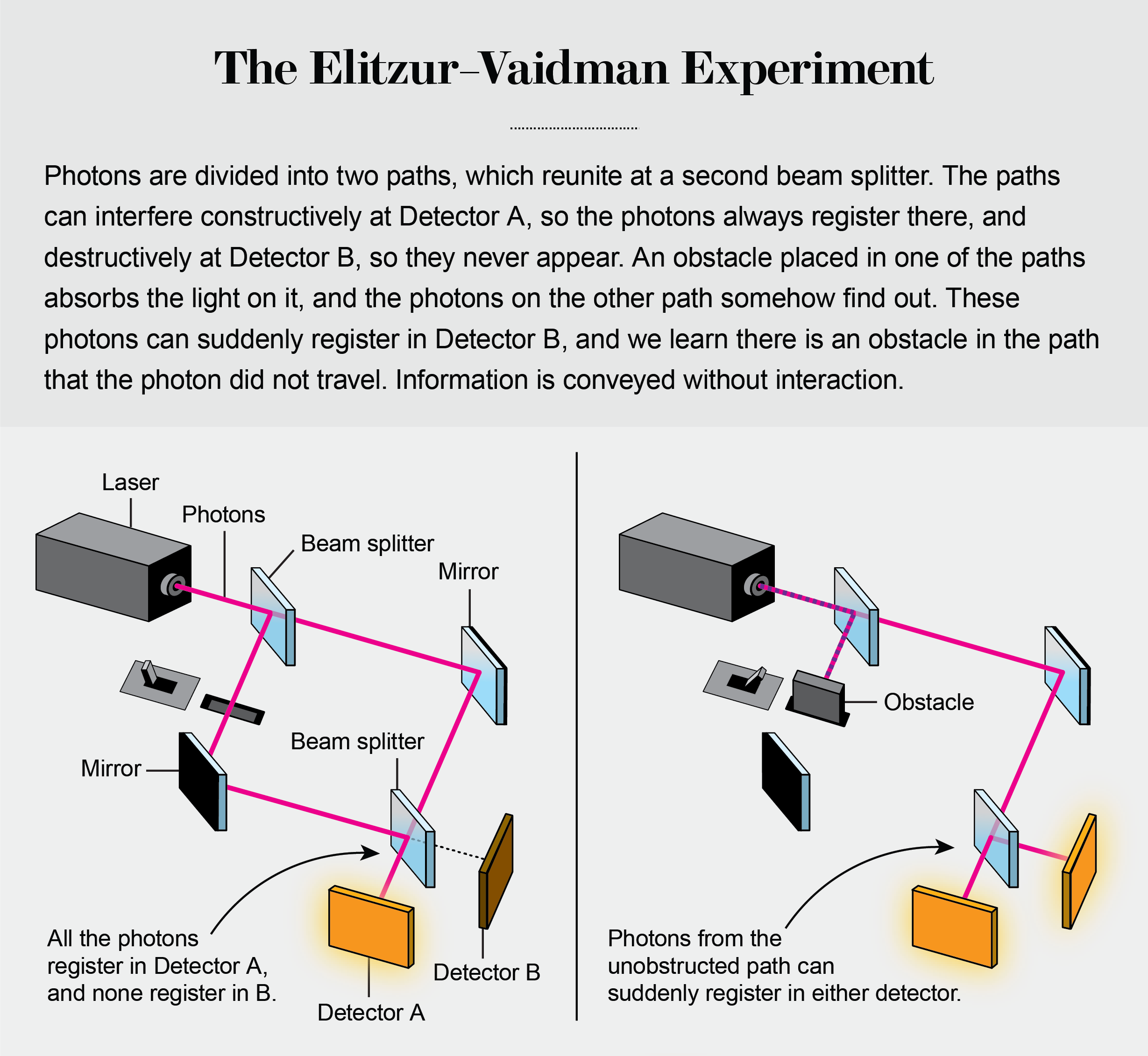
In 1993, Avshalom Elitzur and Vaidman pushed interferometers past the surreal and into the absurd, with a thought experiment that others would make real. Instead of a fluorescent screen, imagine a second beam-splitter where the paths reunite (Figure 2a). Now place a detector in line with each possible path after the splitter. The photons are equally likely to proceed to either detector. Alter one of the original paths again by adding a pane of glass, so there is destructive interference at one detector but not the other—a photon always registers in the second detector, but never in the first. We can actually observe this.
Now place an obstacle in one of the paths after the original split. Half the photons are absorbed and the other half travel the unimpeded path. These unimpeded photons should proceed as before, to the second detector. They do not. Half register in the first detector, which did not click when there were two paths (Figure 2b). The interference disappears because the other path is no longer possible. The photons definitely travel the path without the obstruction, but somehow they know what happens to the other path and change their behavior accordingly. In fact, a photon appearing in the forbidden detector—just once—is enough to intuit the presence of the obstruction.
That's so weird!!
During the 1970s, two physicists at The University of Texas at Austin, Baidyanath Misra and E. C. George Sudarshan, studied the weird capacity for repeated measurements to prolong quantum effects. They called it Zeno’s paradox for quantum mechanics. The Greek philosopher had argued that measuring the position of an arrow repeatedly, as it progresses half the distance to its mark, implies the arrow never lands. Half a distance always remains.
After analyzing the experiment for several months, Vaidman explained that “the photon did not enter the interferometer, the photon never left the interferometer, but it was there.” The particle had to be where it could not, if information was derived from the absence of an object. Kwiat wrote that Vaidman’s interpretation is “nonsense.”
I blogged on it before but it is well worth studying further.

No comments:
Post a Comment