Let's look at the Chinese harmonics that are converted to Hertz.
http://users.wfu.edu/moran/Cathay_Cafe/G_tar.html
So that is the same as saying 2/3 is 66 hertz of 100 hertz.The first step is to put down a fret that will leave 2/3 of the whole string free to vibrate. If the open string is tuned to 400 hertz, then stopping a fret at the 2/3 mark will provide 660 hertz.
So that is the same 2 Hertz difference that I also calculated. So Dr. Patrick Edwin Moran, a Chinese culture and philosophy professor, who studied physics at Stanford, corroborates my claim.Step twelve uses 2/3 and provides about 892 hertz. Note that the true octave is at 880 hertz. Using this system would never permit derivation of the true octave.
I am asked online – is an octave a doubling of Hertz or not? I
have pointed out that this is precisely the “bait and switch” issue that
was covered up: Instead of an inversion of the frequency and
wavelength (as non-commutative subharmonic) there has to be a doubling
of the fraction first to hide the non-commutative relation of the
Perfect Fifth and Perfect Fourth. Music is in time not space – any
musician knows that the G to C interval is a Perfect Fourth – not a
Perfect Fifth. So the 200/300 Hertz interval is 66 Hertz while the
300/200 hertz interval is 150 hertz. So that 66 Hertz is F to 100 Hertz
as C – a Perfect Fifth subharmonic. 150 Hertz is the Perfect Fifth as C
to G. The same C and so it's non-commutative (2/3 as F to C and 3/2 as C
to G).
Now the question is repeated: Is there a doubling of octaves or
not with frequency? O.K. so for Hertz again on the Harmonic Series – it
is 3/2 since the “root” frequency is 100 Hertz and it is the “root”
frequency that is doubled as the octave; So then G to C as 4/3 can’t be
used as the Perfect Fourth; It is inconsistent with the “root” frequency
as 1 or 100 hertz. The 3 is not the “double” of 1 or 2. In other words
in the same scale if G to C is 4/3 then why is G to C as 4/3 in the
harmonic series not allowed for defining the Perfect Fourth? So instead
the subharmonic of 1 as the Harmonic Series or 100 Hertz is used as
2/3x or C to F in the opposite direction – a longer wavelength. So we
can just ignore that it is C to F as the Perfect Fifth in one direction
while it's C to G as the perfect Fifth in the other direction?
I have been asked if this meant that the subharmonic was a subset
of 3/2x and I answered yes. Harmonics are perceived as pitch intervals
and not just Hertz frequency. So it’s been stated then that using “F” as
the new root frequency for doubling the octave you still get – close
to, but not quite the doubling of the octave of 100 hertz as C. Let’s
check the Hertz: 132 plus 66 = 198 Hertz. Yep it's almost the same as
200 Hertz. It’s two Hertz off – exactly the same difference as the error
of time-frequency uncertainty with the truth of the “infinite spiral of
fifths.” I’ll repeat from above, Physicist Iori Fujita: “But even Δt is 1.000 sec, the bandwidth remains about 2 Hz.”
“But even Δt is 1.000 sec, the bandwidth remains about 2 Hz.”
So the point that Alain Connes is making - and the same point that I realized intuitively - is that this difference is due to noncommutative phase as a mathematical structure, not based on any specific numbers.
When Δν is 0.1Hz, Δt should be more than 1 /(4π *0.1) So we can see that Hertz inherently means symmetric phase of 4π
So that is why Connes describes the Quantum Sphere as 2, 3, infinity. So now to your other question. We listen FASTER than Fourier Uncertainty - so we can hear the exact frequency of 2/3 even though it can not be precisely calculated. This is because listening as perception is quantum coherence - at the sub-angstrom wavelength.
So 66 x 2 = 132.
See the 2/3x - that is an F and then the 4/3x is also an F. So you double the first F.
So you have "rounded up" the decimal - but the 10-based number system assumes a divide and average math based on 0 as a negative infinity. rather 66 as 2/3 of 100 is not a decimal fraction. So if you want to expand to the decimal level - that changes how much time is needed to measure the precision of the frequency based on the time-frequency uncertainty of quantum physics. That is the reference I gave: Physicist Iori Fujita:
http://www.geocities.jp/imyfujita/wtcuncertain.html
When Δν is 0.1Hz, Δt should be more than 1 /(4π *0.1) sec which is about 0.80 sec.
Middle C of the equal temperament is calculated approximately as 261.6256Hz. If you want to determine C with this precision 0.0001Hz, you need Δt of 800 sec, or 13 min 20 sec. If you want to get the exact Middle C, you need an infinite time and a continuous wave of C.
In other words, theoretically we cannot get the perfect fifth tone with a frequency f ( that is ν ) from a root tone with a frequency f0 by calculating f = f0 × 3/2.
So here again the error is to assume that the ratio is the same as the frequency. The frequency is actually 3 or 3/1. So as I first discovered this issue, while in high school, by reading Sir James Jeans, the quantum physicist, author of Science and Music he describes the Pythagorean Comma as the difference between 3 to the 12th and 2 to the 7th.
O.K. I will have to refer to my blog for details.
"The value is 129.75 as 12 steps of the fifth while the frequency of the last C as the octave is "128 times that of our starting-point, so that our twelve steps slightly overshoot the mark."
So I will post this - so that above definition of the Pythagorean Comma is not how it is defined based on the logarithmic math.
So you have 8 to the 6th power and 9 to the 6th power (531441) based on the rule of doubling/halving for octaves but the ONLY way that the Perfect Fifth - the Perfect Fourth = 9/8 and the Perfect Fifth + the Perfect Fourth = the Octave is to define the Perfect Fifth and Perfect Fourth not as the fractions 3/2 or 2/3 but as the logarithms of 3/2 squared being 9/4 with the Octave 2 defined as the Geometric Mean Squared. This is the subtle difference between multiplying as doubling and squaring as geometric mean.
So as I have explained - from Professor Richard McKirahan we learn how Philolaus had to flip his Lyre around so that 3/4 as the Perfect Fourth is the wavelength of 0 to 8 root tonic as 1 while 4/3 is the geometric magnitude of 8/6 as the root tonic of 12 to 0 in the opposite direction as 1. So the question is - is 1 a square inherently as geometry? or is 1 a number that can not be seen but rather listened to. The Orthodox early Pythagoreans taught that 1 is NOT a number but originates from female formless awareness as time that is both odd-even at the same time and "breathes" as the void, creating the One as Light. Math Professor Louis Kauffman understands that 1 originates as a noncommutative time series. I have corresponded with Math professor Louis Kauffman about this, as he was a collaborator with quantum psychologist Eddie Oshins at Stanford Linear Accelerator Center.
Scientific Essays In Honor Of H Pierre Noyes On The Occasion Of His ...
Kauffman Louis H, Amson John C - 2013 - ScienceThe special synchronization is the algebra of the time shift embodied in ηη = 1 and [a, b]η = η[b, a] that makes the algebra of i = [1,−1]η imply that i squared = −1.
Since the radian is a dimensionless unit, the radian per second is dimensionally equivalent to the hertz—both are defined as s−1. This may lead to confusion between the quantities angular frequency ω and frequency ν.
Which means this is a 4-dimension vector as spin 1/2 that has to be "converted" to symmetric radians from logarithms.
The stipulation is given in parenthesis - even though it's a MATH website - as it if doesn't really matter:
(start counting at zero):Oh yeah? REALLY? Now the Harmonic Series in math starts at 1 and diverges but still defines frequency as square root of wavelength divided by PI (assuming commutative phase time).
So for Hertz the frequency is actually defined as the square root of the wavelength divided by PI - it is already assumed to have the symmetric logarithmic math.
And so then when we turn to Chinese music tuning we get this strange "exception."
>With the exception of B#, or the ditonic comma,[10] ratio 531441/524288, Table 11.2 shows that the Chinese and Pythagorean progression of ratios are identical, which means that both sequences form an ascending spiral of “fifths.”
>In other words - as you claim - the Fifth and Octave both have a denominator two - and so can be "divided back" - if you use instead of 2 to the 7th power, rather 2 to the 19th power (by adding the logarithms of 12 plus 7 from the 3/2 and the 2/1).
This ratio, 129.75632 : 128 is the Pythagorean comma. 12 perfect fifths do not equal up to 7 perfect octaves:
(3/2)^12 ≠ (2/1)^7 or you could say (3/2)^12 / (2/1)^7 ≠ 1.The problem with just adding these logarithms is you have the SAME "bait and switch" that I am referring to - that is noncommutative. this is why the Chinese and Pythagorean tuning does not use the same definition of the Comma. Because 2/3 is ALSO the PErfect Fifth - not just 3/2.
So this definition, as Alain Connes points out - as I quoted above - actually originates from the noncommutative quotient - the division is noncommutative since 2/3 AND 3/2 are both the Perfect Fifth.
And so rather it is just 3/2 to the 12th and 2/1 to the 7th that is the proper definition of the Pythagorean Comma since it does not assume you can just divide and "average" or then "halve" the fifth back into the octave.So we can see that already with Philolaus - the logarithms as geometric magnitude are assumed in the math.
Lore and Science in Ancient Pythagoreanism
Walter Burkert - 1972 - Literary Criticismto this, the apotome would be 2187: 2048, and the komma 531441 : 524288 — pure frivolity.41 Philolaus' treatment is different:42 He establishes as the basis of tone the number which first makes the cube of the first odd number and was highly honored among the Pythagoreans [i.e., 27] ... a number which is separated by a ...The Science of Harmonics in Classical Greece
Andrew Barker - 2007 - PhilosophyIt is again obvious that Philolaus is not thinking in terms of ratios alone. The ratio of the komma can be computed;it is 531441:524288, but this–in Burkert's phrase– is 'pure frivolity'.21 Boethius has already told us, in fact (Inst. mus. 3.5), that Philolaus identified the komma [531441 : 524288 aka the Ditonic Comma] with the unit, 1, as being the difference between a diesis ...From the Beginning to Plato - Page 269 - Google Books Result
Christopher Charles Whiston Taylor - 1997 - ReferenceThe 'diesis' should be 256:243 and the 'comma' 531441:524288. Neither of these intervals can be divided in half in the sense of the Sectio Canonis. Since Philolaus seems clearly to recognize that the tone cannot be divided in half, it is rather surprising that he apparently takes for granted—what is false in terms of the ..
So then it is assumed that the octave is already defined as the geometric mean squared - which is where Archytas got his equation (Arithmetic mean x harmonic mean = geometric mean squared). So that the 3/2 is actually the arithmetic mean and it can not be 2/3 even though both are the Perfect Fifth. And 4/3 is the Harmonic mean but it was DERIVED from 2/3 that was doubled - and so originally the Harmonic Mean was called the Subcontrary Mean by Philolaus.
So then you get 6 whole tones as 9/8 - being greater than the octave by the so-called Pythagorean Comma. But again this is not the original Pythagorean Comma! This already assumes the octave is a geometric mean squared definition - not the number 2 as a doubling.
So you have 8 to the 6th power and 9 to the 6th power (531441) as the secret of the Ditonic Comma as the fake Pythagorean Comma due to geometric mean. From Euclid and earlier from Philolaus and Archytas as 8 to the 6th compared to 9 to the 6th which assumes that the starting root tonic "frequency" as the 1 is 8 to the 6th which is already from assuming the Perfect Fifth is squared!

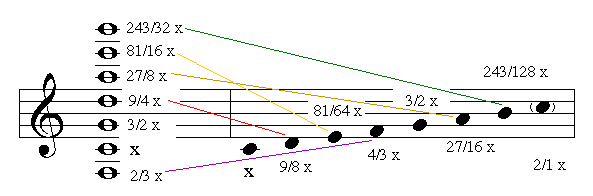
No comments:
Post a Comment