The Non-commutative Fibonacci Cantor Set of Alain Connes as 2, 3, infinity secret of alchemy meditation and quantum computing logic gate

So I was having an open discussion with a relative about music theory and the secret power of music and how it is related to math and psycho-physiology and the paranormal and spiritual, etc. And the relative mentioned the Fibonacci Series. I said YES but NOT the Golden Ratio. So then during my past week of meditation I realized that the Fibonacci Series MUST be non-commutative. I then began working out of the math, how it relates to music theory. I actually delved into this already in my 2012 pdf, Alchemy of Rainbow Heart music.

So I reviewed that research.

And I searched non-commutative Fibonacci. Sure enough it turns out to be considered a secret to developing quantum computing.

But before I go into that - I realized there must be more to this based on my own take. Sure enough Alain Connes does go into this as well!





So this is very fascinating. I had never NOTICED this aspect of Alain Connes research pdf (A walk in the noncommutative garden).

So we can see how the above is not quite the same as the typical Cantor Set:




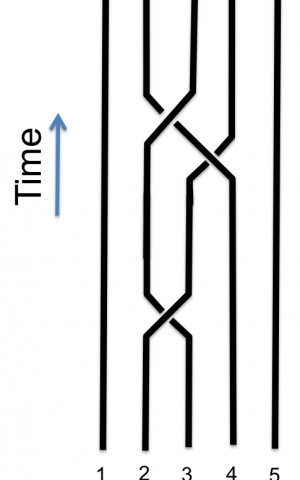
So now look at the quantum computing example. We can assume this is connected to Connes research as he promotes quantum computing and this is noncommutative research:

Now let's look at my own research on this:

First that article:

'Fibonacci quasiparticle' could form basis of future quantum computers...

Also, movements of the anyons must be non-Abelian, a property similar to the non-commutative property in which changing the order of the anyons' movements changes their final tracks. In most proposals of TQC so far, the non-Abelian statistics of the anyons has not been powerful enough, even in theory, for universal TQC.
Now in a new study published in Physical Review Letters, physicists Abolhassan Vaezi at Cornell University and Maissam Barkeshli at Microsoft's research lab Station Q have theoretically shown that anyons tunneling in a double-layer system can transition to an exotic non-Abelian state that contains "Fibonacci" anyons that are powerful enough for universal TQC.

So the article says it's a new type of non-commutative quantum logic gate....

So you look at that image and consider what I wrote based on my meditation.

1=C=2=4=1=C

Logarithms not allowed so 3:4 Perfect 4th =G:C (octave) is not allowed since 1 is as 3 is not the same root tonic for the overtone series

And then 1:2::2:3 is the Fibonacci series

So therefore it has to be non-commutative.

Now I didn't rewrite all my notes but that is enough.

Now look at the above image again - it clearly encapsulates the Non-commutative music exchange harmonics of 1:2:3:4

That is the article of the science research

Fibonacci anyon excitations of one-dimensional dipolar lattice bosons

T Đurić, K Biedroń, J Zakrzewski - Physical Review B, 2017 - APS

… Such states and their quasiparticle excitations are therefore called non-Abelian or noncommutative …
An example of such non- Abelian states are the states that support SU(2)3 Fibonacci anyon
quasiparticle excitations [2–4]. The final result of the computation, that is the final … 

 

 https://arxiv.org/pdf/1802.06176.pdf

So follow-up research cites Kauffman and Aharonov. Fascinating.

 

 So this is an upside down version of the above image.

So now we can see the "power" of this simple yet previously "neglected' or covered up non-commutative phase logic idea! I previously cited a research group using music theory directly for developing quantum computing - as non-commutative logic. Here we see it as a topology of the same logic.

And then there are scientists who think the Universe is really a quantum computer. Well the logic is switched around! We do not NEED to build a quantum computer if we already inherently are one! the ancient alchemists figured this out already!


In fact I told my relative that all we need to know for math is 2, 3, infinity and they smiled and laughed - well now I have the proof!