I don’t follow at all. What’s 4/3 got to do with 3 not going into 2?
O.K. so you have to consider the pitch along with the geometry. So first of all we have 4/3 with 3 as the root tonic as an overtone but if 1 is the root tonic then there is no way that 3 can be the denominator for the overtone of the 1 as 4/3. So then Western science instead uses the harmonic series and so 4/3 is just a "ratio" as 4:3 and so the order supposedly doesn't matter - since it is supposedly symmetric math or commutative. Now the problem with this is again the pitch. So 4 is actually the same pitch as 2 meaning the octave of 1 as C in geometry. And yet when you consider the C as the same octave in pitch then 3/4 is G to C (octave) while 4/3 is C (root tonic) to F. Both are the Perfect Fourth but have a different geometry that is noncommutative. And again this is why the pitch pipes are radically different than using a string - because the Daoists and early Pythagoreans are then taking 4/3 "wavelength" of 2/3 frequency but obviously you can not take a wavelength greater than 1 - so it would be physically impossible using a string. So the Greeks in trying to line up the 3 with the 2 were forced to use a double octave that then changes the direction of the "1" and also hides the change in the fundamental pitch - and then called this the Greater Perfect System (of the double octave) by just calling the pitch a ratio. Whereas the empirical truth that Pythagoras realized is that frequency is inverse to wavelength or time and vice versa.
But then why do they say that the perfect fifth is harmonic with the octaves? Listening to the perfect fifth and the root tonic sounds very harmonic, so why is this so?
So Western science tries to cover this up. It is quite fascinating actually! Western science - since the 1600s with logarithms - has called this the "coincidence of consonances" from low number integer ratios. So I was literally taught in my private training by a former university music professor that there was nothing to this Perfect Fifth/Octave harmonics. And so the "avant-garde" or so called "sophisticated" University music composers were all using computers and fancy math for "serialism" and computer music and then claiming the masses did not like it because they were just "behind the times." haha. Hilarious. I got punished when I laughed a music composition professor and I told him that no one would like that type of music - as he had invited us all to his new house on the prairie in Wisconsin. Anyway I won't go into what happened regarding that story from the early 90s. But science has now validated my view. Neuroscience has shown that the Perfect Fifth/Octave has the strongest amplitude resonance of neurons in the brain. And also all human cultures is the Octave/Perfect Fifth - and more so - even animals besides humans prefer these simple ratios for harmonics.
So this was originally called the Logos as the Pythagorean Tetraktys but it is also the "three gunas" - the oldest philosophy of India and it is the Tai Chi of Daoism - and it goes back to the original human culture as the secret of the N/om kundalini energy. I have been critiquing Adam Neely's popular music theory youtube series - because he is a technocrat. Western music training converts musicians into technicians and so they define time not by listening but by visual measurement of time as a "contained" infinity of 1 as a circle using irrational magnitude numbers. So the reason these simple ratios sound harmonic is as Helmholtz explained - because their overtone harmonics are in resonance based on the overtone series.
You don't need any instrument - pipe, string, etc. - but you can simply LISTEN - and it is proven that the throat singing is actually developed by listening to the highest pitch we hear externally and this resonates the whole brain as ultrasound which activates the vagus nerve. This vagus nerve activation from inner ear high frequency resonance - from flexing the middle ear muscles - then relaxes the throat muscles, thereby enabling the low loud subharmonics of the throat singing. So unless a musician can do throat singing then they have not even enacted this truth of natural resonance harmonics.
So for example in Western singing training - you are taught to do deep belly breathing with the diaphragm. Of course they don't tell you this is also the secret of shamanic internal energy training. O.K. so what science has discovered is that for humans, along with birds, our auditory cortex is very close to our motor cortex and frequency sound as music is stored in the right brain with strong vagus nerve activation - via the cerebellum that coordinates both emotions and motion as the motor cortex. So real harmonic music is innately tied to dancing as synchronized movement. Birds can do this but most animals can not - and humans can also do synchronized body motions to a steady rhythm. So in fact, as some music Ph.D. analysis has shown - and I have corresponded with Professor Daniel Oore about this - the syncopated rhythm is process as more right brain dominant.
Normally, as science has shown, the human brain processes timing perception in the left brain and frequency perception in the right brain - and so there is a supposed "trade off." But what is not recognized is that right brain listening synchronizes the left brain because the right side vagus nerve connects to the left brain. But left brain dominant listening (as in speech with right hand dominance) does NOT synchronize the whole brain since the left side vagus nerve does not connect to the right side of the brain. So it is counterintuitive. The psychologist Stan Gooch got into this by emphasizing the cerebellum - which actually has a greater prefrontal cortex relative to its size, compared to the cerebrum brain. His book "Total Man" goes into this. I corresponded with Stan Gooch as he had "retired" to a caravan trailer in Wales and then he died there. But he had some amazing paranormal experiences and so he switched his psychology research to paranormal training and he argued that modern humans are basically mass mind controlled since we lost touch with how to activate our cerebellum.
O.K. so sorry for rambling here - but the other thing is that it is a "mystery" to science why humans recognize a "pitch centre" - or center - called "pitch centre recognition." But you have to realize that scientists are projecting the WRONG math back onto the music and then claiming they don't understand this mystery! haha. This is why math professor Joe Mazur wanted me to publish my music theory research in a math journal but since I was critiquing the foundation of math, of course my research was rejected without comment. But the math of "noncommutative phase" is increasingly being recognized - and as Alain Connes emphasizes - this is the proper math of music theory as the empirical truth of natural harmonics.
Science has now proven that the sound we hear as language or thinking inside our heads originates as an electromagnetic wave that has the SAME form as the sound that is produced. So in other words concepts as thinking originate as electromagnetic sound forms (or acoustic oscillations as quantum phonons) or phase wave forms. It is as in holography - the form as phase is based on synchronized frequency of the laser. So it is called "super-radiance" that self-amplifies based on the frequency/time resonance.
So quantum physicist Fred Alan Wolf describes the "quantum jump" as natural harmonics from "beats" of subharmonics and overtones:
The movement of the electron from one orbit to another lower energy orbit was a simple change of notes. As a violin string undergoes such a change, there is a moment when both harmonics can be heard. This results in the well-known experience of harmony, or as wave scientists call it, the phenomenon of beats. ...The light was a beat, a harmony, between the lower and upper harmonics of the Schroedinger-de Broglie waves. When we see atomic light, we are observing an atom singing harmony....They had no medium to wave in, and they had no recognizable form in physical space.
So what has to be recognized is that there is a "direction" to time - and so what de Broglie realized - when he analyzed relativity in contrast to quantum energy - is that there HAS to be two directions to time - at the same time. This is the "Law of Phase Harmony" - so that then the 2/3 and 3/2 are at the SAME time. What the Daoists stated then, along with the early Pythagoreans and the philosophy of the "three gunas" is that is it the "three gunas of no guna" or "there is no one or no 1" or it is just "undivided yin-yang" so that we are self-amplifying as the Yuan Qi directly but we can only "perceive" it through light as our spiritual ego - the invariance of the speed of light to make a visual measurement of time. And so the 3/4 or 4/3 then changes in relation to the 1 but the 1 also changes in value as a spacetime shift of infinite consciousness that is formless as the yuan qi or Shakti Nada - the "sound-current nondualism."
Here is how Manfred Euler, a physics professor in Germany describes it - in my correspondence with him:
"Universal coherence" - a "mind boggling outlook."Sitting in a quiet room, we can hear sounds that cause our eardrums to vibrate by less than the diameter of an atom. ...
Phase harmony in de Broglie theory relates a local periodic phenomenon (the 'particle clock') to a periodic propagating field in such a way that relativistic invariance is satisfied. If a similar phenomenon in the cell is relevant it should couple the global oscillation pattern locally with periodic (mechanic, electric, biochemical ???) processes.
Coherence as consciousness.
"Ghost Tones"
Manfred Euler is a Professor Emeritus of Physics at the University of Kiel.
Quantum Effects in the Dynamics of Biological Systems, 1983, Lawrence Berkeley National Laboratory, William Bialek (currently Princeton Professor)
Here is the "mystery" that mainstream science is stopped at since it does not understand noncommutative phase mathematics:
The Nature and Nurture of Musical Consonance (PDF Download Available).
The most frequently used intervals—the octave,perfect 5th and 4th—correspond to those considered the most consonant by culturally diverse listeners (Bowling & Purves, 2015; Burns, 1999), an observation that is all the more impressive given that the frequency resolution of the human auditory system is sufficient to distinguish hundreds of unique intervals (Parncutt, 1989; Roederer, 2008).
A biological rationale for musical consonance
The basis of musical consonance has been debated for centuries without resolution. Three interpretations have been considered: (i ) that consonance derives from the mathematical simplicity of small integer ratios; (ii) that consonance derives from the physical absence of
interference between harmonic spectra; and (iii) that consonance derives from the advantages of recognizing biological vocalization and human vocalization in particular. Whereas the mathematical and physical explanations are at odds with the evidence that has now accumulated, biology provides a plausible explanation for this central issue in music and audition.
And since the perfect fifth cannot go into the octaves by themselves (as explained above), they are required to be multiplied by 4/3 (perfect fourth) to arrive at the next octave (and by this reasoning, a root tonic multiplied by 3/4 arrives at the perfect fifth of the octave previous). This is why, to reach the next octaves, the Daoists used 3/2 (yang) and multiplied it with 4/3 (yin). Am I understanding you correctly?
https://www.persee.fr/doc/oroc_0754-5010_1994_num_16_16_994
Celestial Cycles and Mathematical Harmonies in the Huainanzi
[article]
Extrême-Orient, Extrême-Occident Année 1994
O.K. so as he describes it - the 2/3 and 4/3 wavelength
alternation still increases each note "by the power of 3" - meaning
based on the Perfect Fifth. But the crucial difference from trying to
line it up with the Octave is to remember that the pitch is
noncommutative - so that 3/4 is the frequency of 4/3 which is C to F
while 2/3 is the frequency 3/2 which is C to G, and so on.
So again what we need to realize is that Western mathematics is
now "imposed" onto Chinese tuning - just as it is imposed on early
Pythagorean tuning and the three gunas tuning from India. So in the case
of Daoist harmonics - there are different claims being made. One is
that the Daoists never tried to line up the Perfect Fifth with the
Octave - because the root tonic was never defined as a "ratio" whereas
in the West the root tonic or 1:2 was defined as (x squared). But all
these claims of musicologists ignore the fact that for the Daoists - the
root tonic was actually the lunar energy as the 9 number of growth. So
just as with the Pythagoreans the Tetrad is of 2:3:4 = 9 as eternal
yin-yang resonance as qi energy.
So if you look at my blog - http://elixirfield.blogspot.com/2018/04/is-there-right-and-wrong-in-music.html
This post - I have an image from Alain Connes - describing this secret
of yin-yang at a zero point in spacetime. So there really isn't any zero
in time but rather an infinite yin-yang at the zero point in space -
with the time from the future and the past being harmonized and light is
the spiritual ego that perceives this harmonize as a direction of time.
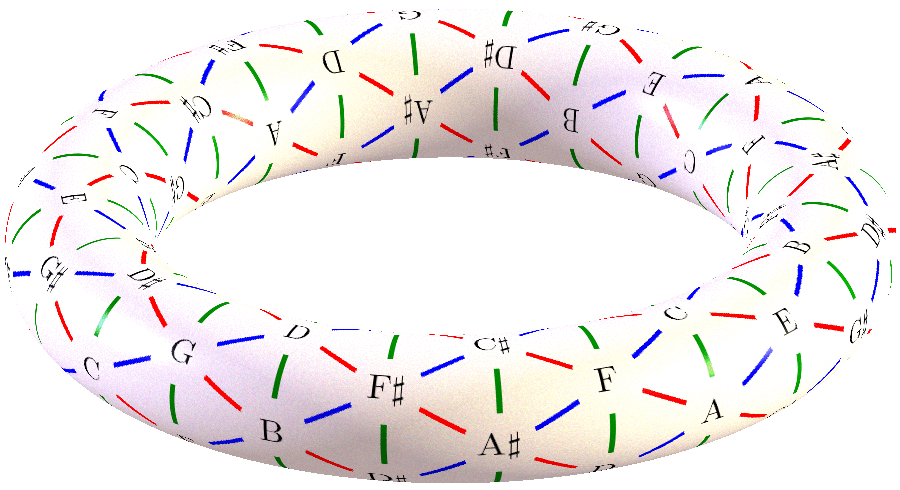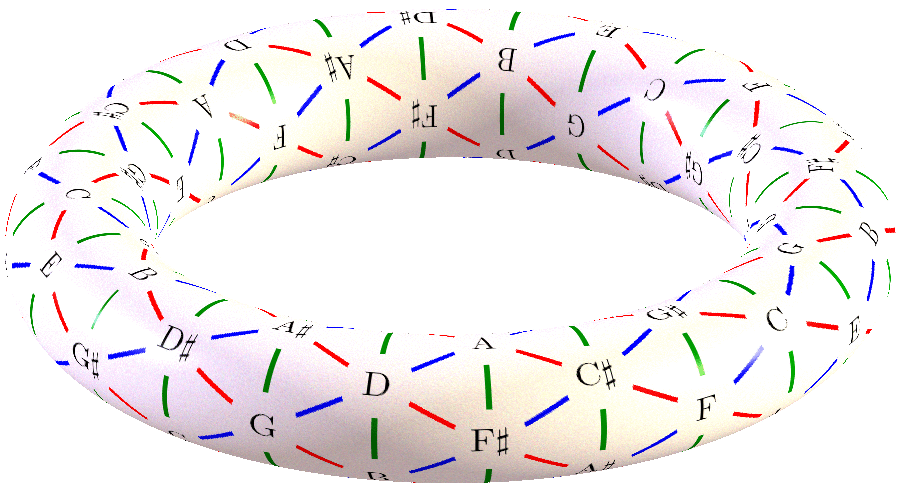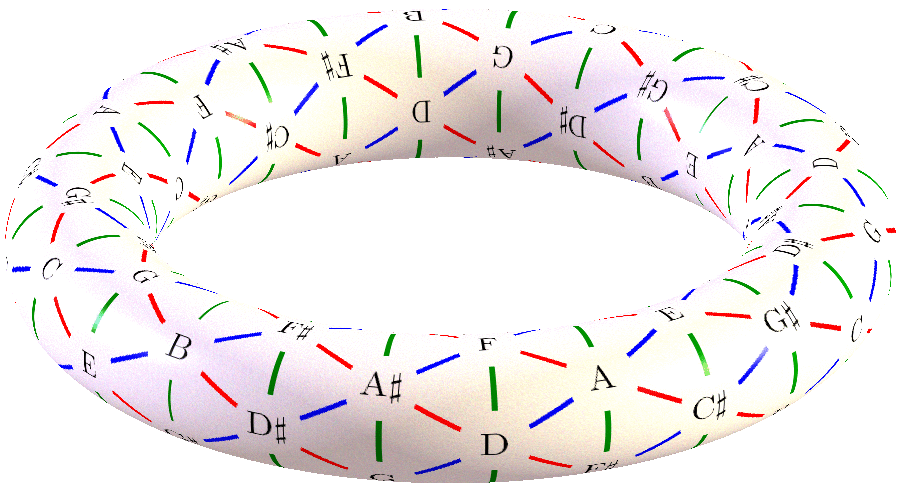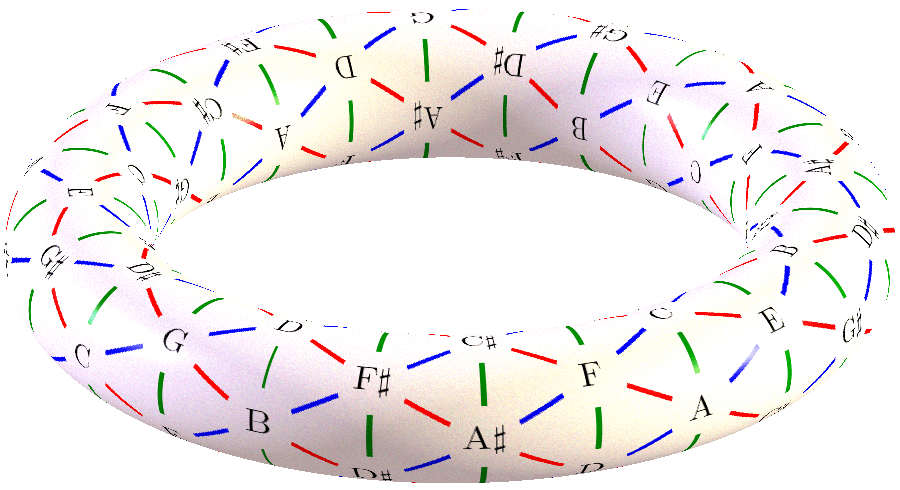
So this is the limit of WEstern tuning - you can see it is the Perfect Fifth as a torus design but this still tries to "contain" the infinity into a closed geometry - and so it still has the "commas" inherent to it and the "comma" value changes based on the direction of the time.

So you can see what Alain Connes does - is he is stating that at each "zero point" in that torus there is still a 5th dimensional yin-yang or (2, 3, infinity) frequency spectral. That is the real secret of the Daoist harmonics or Pythagorean Tetraktys or the three gunas.
I typed 3/2 x 4/3, and 3/2 + 4/3 into my calculator and they both arrive at 2. Why is it a lie? Why does the root tonic have to be changed to accommodate it? I don’t understand. Assuming you keep the numbers irrational before you arrive at the answer, I don’t see the problem in adding?
Yes maybe your calculator is assuming logarithms? But if it is just fractions then they are not the same. The logarithms assume that time is contained as a spatial measurement. Listening belies this, as does the empirical truth of the harmonics, as Sir James Jeans points out. The Harmonic Series "diverges" and so was called the "invention of the devil" by mathematicians - what this means is also called the Devil's Interval for chaos resonance. Engineers like irrational numbers since it cuts off the natural resonance but if you use the natural resonance numbers then the physical form "diverges" - meaning self amplifies into the apparent self-destruction of the physical form. I go into this in my Devil's Interval music harmonics article. http://ecoechoinvasives.blogspot.com/2017/05/my-last-blog-saved-by-ancient-knowledge.html
But if it is a lie, and the Daoists thought so, why did you share a Daoist drawing of the circle of fifths (second picture of this thread)? If they believe it to be a spiral (or just not the circle of fifths), then why did they draw a circle of fifths?
This is the same reason that the microcosmic orbit is also a closed "circle" as meditation. The harmonics only "appear" to return but each cycle is a spacetime transformation and so just as we can not "see" the Wuji - even though it is shown as a circle - we can only listen to the real tai chi harmonics or taji.
I’m sorry, I don’t quite follow here. Why does the perfect fourth change the root tonic? And didn’t you say that it’s bad music theory to change the root tonic?
I am asked online – is an octave a doubling of Hertz or not? I
have pointed out that this is precisely the “bait and switch” issue that
was covered up: Instead of an inversion of the frequency and
wavelength (as non-commutative subharmonic) there has to be a doubling
of the fraction first to hide the non-commutative relation of the
Perfect Fifth and Perfect Fourth. Music is in time not space – any
musician knows that the G to C interval is a Perfect Fourth – not a
Perfect Fifth. So the 200/300 Hertz interval is 66 Hertz while the
300/200 hertz interval is 150 hertz. So that 66 Hertz is F to 100 Hertz
as C – a Perfect Fifth subharmonic. 150 Hertz is the Perfect Fifth as C
to G. The same C and so it's non-commutative (2/3 as F to C and 3/2 as C
to G).
Now the question is repeated: Is there a doubling of octaves or
not with frequency? O.K. so for Hertz again on the Harmonic Series – it
is 3/2 since the “root” frequency is 100 Hertz and it is the “root”
frequency that is doubled as the octave; So then G to C as 4/3 can’t be
used as the Perfect Fourth; It is inconsistent with the “root” frequency
as 1 or 100 hertz. The 3 is not the “double” of 1 or 2. In other words
in the same scale if G to C is 4/3 then why is G to C as 4/3 in the
harmonic series not allowed for defining the Perfect Fourth? So instead
the subharmonic of 1 as the Harmonic Series or 100 Hertz is used as
2/3x or C to F in the opposite direction – a longer wavelength. So we
can just ignore that it is C to F as the Perfect Fifth in one direction
while it's C to G as the perfect Fifth in the other direction?
I have been asked if this meant that the subharmonic was a subset
of 3/2x and I answered yes. Harmonics are perceived as pitch intervals
and not just Hertz frequency. So it’s been stated then that using “F” as
the new root frequency for doubling the octave you still get – close
to, but not quite the doubling of the octave of 100 hertz as C. Let’s
check the Hertz: 132 plus 66 = 198 Hertz. Yep it's almost the same as
200 Hertz. It’s two Hertz off – exactly the same difference as the error
of time-frequency uncertainty with the truth of the “infinite spiral of
fifths.” I’ll repeat from above, Physicist Iori Fujita: “But even Δt is 1.000 sec, the bandwidth remains about 2 Hz.”
But don’t 3/2 and 2/3 have the same size interval? So why would subtracting the perfect fourth (3/4) from values of equal size make any difference? 3/2 is using the perfect fifth interval to increase the frequency from the tonic root by x amount, and 2/3 is using the perfect fifth interval to decrease the frequency from the tonic root by x amount. I know that 3/2 = 1.5, and 2/3 = 0.66, but it is a ratio. Like going up a ladder of certain length from the ground (tonic root), and then coming back from the top down to the ground (tonic root).
The rest I think I understand, as you explained very well. I’m very grateful for you taking the time to explain this difficult topic to us. Thank you
O.K. so now I'll answer your question about Philolaus - and the cognitive bias of WEstern science using logarithmic as irrational numbers - from music theory.
Professor Richard McKirahan reveals the secret:
Or as Professor Borzacchini states:
The word translated epogdoic is not a musical term but a mathematical one. An epogdoic ratio is the ratio of 9 to 8. The occurrence of a mathematical term here is unexpected. It has been treated as an unimportant anomaly but in fact it is the key to the entire fragment....The word magnitude normally refers to physical size, but here it is given a new application, extending the notion of magnitude to include musical intervals.
Yes Philolaus taught that a "double octave" is necessary to create music theory with 0 to 6 as first octave and 6 to 12 as second octave and then the wavelength is reversed. So 3/2 is the first harmonic as C to G overtone, Perfect Fifth but then 8/6 is the 2nd harmonic as 4/3 frequency from 6/8 or 3/4 wavelength that is really the 2nd octave! See the bait and switch! This then enabled Archytas to claim that Perfect Fifth plus Perfect Fourth = the Octave since the arithmetic mean x harmonic mean = geometric mean squared or 3/2 x 4/3 = 2. Notice that 2/3 is also the Perfect Fifth as C to F subharmonic - but that can no longer be used based on the lie of ARchytas. So everyone learns the wrong music theory based on symmetric math when the truth is noncommutative phase or G=3=F at the same time as complementary opposites of overtones and subharmonic undertones. This is why if you learn music through singing and listening - then a person creates subharmonic undertones with throat singing and vowels as mantras create overtone harmonics. The older language is the more musical it is and so no instrument - no wavelength, no tube or pipe - is necessary. We listen to music and this reveals its true secrets whereas the logarithmic math of ARchytas music harmonics is a lie that covers up the fact that C to F 2/3 Perfect Fifth is also C to G 3/2 Perfect Fifth. This is called the "Ghost tonic" in music theory since the Perfect Fourth is not part of the harmonic series.These remarks raise the question of the difference between the ancient Pythagorean ‘musical’ perception as displayed in the Pythagorean idea of ‘linear number’ in Boethius [Philolaus] or in Nicomachus, and the modern ‘geometrical’ perception of the linear numerical magnitudes.
yes that last section I didn't follow explain. So this is from Richard McKirahan, professor, his article, ON Philolaus and Number. So the 3/2 frequency as C to G is 8/12 wavelength with the root tonic or fundamental pitch as 0 to 12 as 1. Then 6/8 is the 3/4 wavelength with 4/3 as the frequency with 0 to 8 at the root tonic or fundamental pitch for C to F. So see the bait and switch of the "1" - and so this is so it can be converted to geometric magnitude - so then 9/8 is the fundamental x as a math ratio of geometric magnitude. So then 12 to 8 is 3/2 as geometric magnitude as 8 to 6 is 4/3 as geometric magnitude (logarithms). So then 3/2 plus 4/3 = 2 frequency as the octave of 12 to 6. But in fact this octave is geometric mean squared - and so the geometric mean is 9/8 cubed as the major 2nd note. So then 9/8 is the logarithmic subtraction of 3/2 - 4/3 as logarithms. But again the Perfect Fifth can not be 2/3 in this equation - even though it is 2/3 as a harmonic. So the scale is actually built up from 9/8 by assuming that 3/2 can be "halved" back into the octave - evenly with the octave. In other words 3/2 is squared whereas for the Chinese Daoist tuning the multiplication of 3/2 by itself is with the opposite harmonic of 4/3 and they are not "squared" as geometric mean or harmonic mean. So Philolaus called 4/3 the "subcontrary mean" because it was derived from the subharmonic of the Perfect Fifth as C to F - or 0 to 8 with 6/8 as the 3/4 of the root tonic of the Perfect Fifth! But Archytas changed the term to Harmonic Mean instead of subcontrary mean - thereby covering up the fact that Philolaus got it from the subharmonic as the Perfect Fifth, which was a different geometry as C to F, that was noncommutative phase with the fundamental pitch. The Chinese Daoists did not hide this noncommutative phase and instead did not use zero - since zero is a negative infinity based on the idea of containing time as a materialistic idealism of irrational magnitude. This is why Aristotle was against zero and also why Kepler was against the closed form of the golden ratio....

 John S. Major
John S. Major
No comments:
Post a Comment